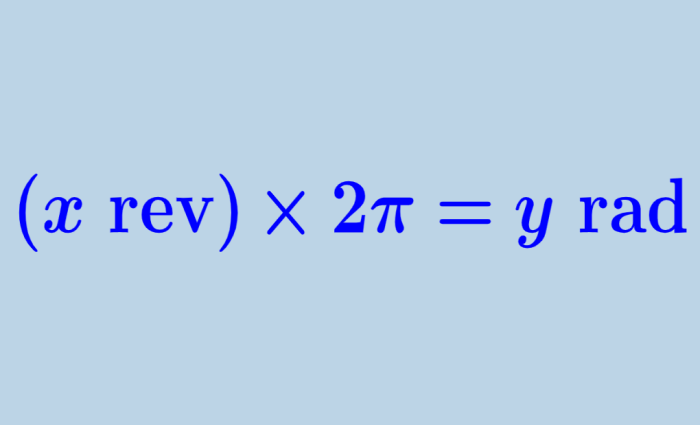Cara mengubah putaran ke radian – Apakah Anda ingin menguasai konversi dari putaran ke radian? Tak perlu khawatir! Artikel ini akan memandu Anda langkah demi langkah untuk memahami konsep ini dengan mudah dan menyenangkan. Mari kita jelajahi dunia matematika dan fisika dengan cara yang lebih mendalam.
Dalam kehidupan sehari-hari, kita sering berhadapan dengan konsep putaran, seperti putaran roda mobil atau gerakan jarum jam. Namun, dalam dunia sains dan matematika, kita juga perlu memahami satuan lain yang disebut radian. Konversi dari putaran ke radian sangat penting untuk berbagai aplikasi, seperti menghitung kecepatan sudut dan torsi.
Konsep Dasar: Cara Mengubah Putaran Ke Radian
Putaran dan radian adalah dua satuan yang digunakan untuk mengukur sudut. Putaran adalah satuan yang menyatakan sudut sebagai pecahan dari lingkaran penuh, sedangkan radian menyatakan sudut sebagai panjang busur lingkaran yang dihasilkan oleh sudut tersebut pada jari-jari lingkaran.
Untuk mengubah putaran ke radian, cukup kalikan putaran dengan 2π. Ini karena satu putaran sama dengan 2π radian. Menariknya, memahami konsep ini sangat penting saat bekerja dengan mikroskop. Memegang mikroskop dengan benar akan memungkinkan kita menyesuaikan posisi lensa secara tepat untuk mendapatkan gambar yang jelas.
Kembali ke topik konversi putaran ke radian, penting untuk mengingat rumus 2π untuk melakukan konversi dengan akurat.
Hubungan antara putaran dan radian dapat dinyatakan sebagai berikut:
putaran = 2π radian
Dengan demikian, untuk mengonversi putaran ke radian, cukup kalikan nilai putaran dengan 2π.
Contoh Konversi
Misalkan kita ingin mengonversi 30 putaran ke radian:
putaran × 2π radian/putaran = 60π radian
Metode Konversi
Mengubah putaran ke radian adalah tugas penting dalam berbagai bidang, seperti fisika, teknik, dan matematika. Ada beberapa metode yang dapat digunakan untuk melakukan konversi ini, masing-masing dengan kelebihan dan kekurangannya sendiri.
Saat mengubah putaran menjadi radian, diperlukan konversi nilai sudut. Proses ini sangat penting dalam berbagai bidang, seperti trigonometri dan fisika. Menariknya, konsep konversi ini juga diterapkan dalam dunia bisnis dan keuangan. Untuk membuat laporan keuangan yang komprehensif dan akurat, Anda dapat memanfaatkan spreadsheet Excel.
Panduan membuat laporan keuangan di Excel dapat membantu Anda mengelola data keuangan dengan mudah. Kembali ke konversi putaran ke radian, konstanta π (pi) memainkan peran penting dalam menentukan hubungan antara dua satuan sudut ini.
Menggunakan Konstanta Pi
Salah satu metode paling umum untuk mengonversi putaran ke radian adalah menggunakan konstanta pi (π). 1 putaran sama dengan 2π radian. Rumus untuk konversi adalah:
radian = putaran × 2π
Misalnya, untuk mengonversi 3 putaran ke radian, kita akan mengalikan 3 dengan 2π:
radian = 3 putaran × 2π= 6π radian
Menggunakan Derajat per Radian
Metode lain untuk mengonversi putaran ke radian adalah menggunakan derajat per radian. 1 putaran sama dengan 360 derajat, dan 1 radian sama dengan 180/π derajat. Rumus untuk konversi adalah:
radian = putaran × 360°/180°/π= putaran × 2π/180°
Untuk mengubah putaran menjadi radian, kita cukup mengalikan nilai putaran dengan konversi π/180. Mirip seperti mengaplikasikan body cream secara merata pada kulit, proses ini melibatkan pengubahan satuan. Dengan mengalikan dengan π/180, kita mengubah satuan putaran yang lebih besar menjadi radian yang lebih kecil, sama seperti saat kita mengoleskan body cream tipis-tipis untuk mendapatkan hasil yang optimal.
Dengan pemahaman dasar ini, kita dapat dengan mudah mengonversi putaran ke radian, memfasilitasi perhitungan dalam berbagai bidang sains dan teknik.
Misalnya, untuk mengonversi 45 putaran ke radian, kita akan mengalikan 45 dengan 2π/180°:
radian = 45 putaran × 2π/180°= 45 × 2π/180°= 15π/6 radian
Kelebihan dan Kekurangan Masing-masing Metode
- Menggunakan Konstanta Pi:
- Kelebihan: Mudah diingat dan diterapkan.
- Kekurangan: Dapat menyebabkan kesalahan pembulatan karena penggunaan pendekatan π.
- Menggunakan Derajat per Radian:
- Kelebihan: Lebih akurat daripada menggunakan konstanta pi.
- Kekurangan: Rumus yang lebih kompleks dan mungkin memerlukan penggunaan kalkulator.
Langkah-langkah Konversi
Mengubah putaran ke radian adalah proses sederhana yang dapat dilakukan dengan mengikuti beberapa langkah berikut:
1. Kalikan putaran dengan konstanta 2π
2. Hasilnya adalah nilai radian
Misalnya, untuk mengubah 1 putaran menjadi radian, kita kalikan 1 dengan 2π:
putaran x 2π radian/putaran = 2π radian
Contoh Praktis
Dalam dunia nyata, konversi putaran ke radian sering digunakan dalam berbagai bidang, seperti fisika, teknik, dan matematika.
Salah satu contoh paling umum adalah dalam menghitung panjang busur lingkaran. Panjang busur lingkaran adalah jarak sepanjang tepi lingkaran, dan dapat dihitung menggunakan rumus berikut:
s = rθ
Dalam fisika, mengonversi putaran ke radian adalah prosedur penting. Untuk mengonversi 180 derajat menjadi radian, cukup kalikan dengan π/180. Mengetahui konversi ini penting untuk perhitungan fisika yang akurat. Namun, dalam urusan perbankan, ada prosedur penting lainnya, yaitu mengganti pin ATM Mandiri melalui ponsel.
Kunjungi cara mengganti pin atm mandiri lewat hp untuk panduan langkah demi langkah. Setelah menyelesaikan urusan perbankan Anda, jangan lupa untuk kembali ke konversi putaran ke radian untuk menyelesaikan perhitungan fisika Anda.
Dimana:
- s adalah panjang busur
- r adalah jari-jari lingkaran
- θ adalah sudut pusat dalam radian
Untuk mengonversi putaran ke radian, cukup kalikan nilai putaran dengan 2π.
Contohnya, jika Anda memiliki sudut 30 derajat, maka dalam radian adalah:
- derajat
- (2π / 360 derajat) = π / 6 radian
Konversi putaran ke radian juga penting dalam menghitung kecepatan sudut dan percepatan sudut. Kecepatan sudut adalah laju perubahan sudut terhadap waktu, dan diukur dalam radian per detik (rad/s). Percepatan sudut adalah laju perubahan kecepatan sudut terhadap waktu, dan diukur dalam radian per detik kuadrat (rad/s²).
Aplikasi dalam Matematika dan Fisika
Konversi putaran ke radian sangat penting dalam matematika dan fisika, karena radian merupakan satuan sudut yang lebih disukai dalam perhitungan. Berikut adalah beberapa aplikasi umum:
Dalam Matematika, Cara mengubah putaran ke radian
- Trigonometri:Radian digunakan dalam definisi fungsi trigonometri, seperti sinus, kosinus, dan tangen.
- Kalkulus:Radian digunakan dalam turunan dan integral fungsi trigonometri, serta dalam konsep limit dan deret Taylor.
- Geometri:Radian digunakan untuk mengukur sudut pada lingkaran, termasuk panjang busur dan luas juring.
Dalam Fisika
- Gerak Rotasi:Radian digunakan untuk mengukur sudut rotasi suatu benda, seperti roda atau pendulum.
- Gelombang:Radian digunakan untuk mengukur frekuensi dan panjang gelombang, serta untuk menganalisis sifat gelombang.
- Teori Relativitas:Radian digunakan dalam persamaan fisika relativistik, yang menggambarkan ruang-waktu sebagai sebuah kontinum melengkung.
Ringkasan Terakhir
Dengan memahami cara mengubah putaran ke radian, Anda telah membuka pintu ke pemahaman yang lebih luas tentang dunia matematika dan fisika. Konversi ini tidak hanya penting untuk menyelesaikan masalah akademis, tetapi juga memiliki aplikasi praktis dalam berbagai bidang, seperti teknik dan navigasi.
Jadi, teruslah berlatih dan jadilah ahli dalam konversi putaran ke radian!
Detail FAQ
Apa perbedaan antara putaran dan radian?
Putaran adalah satuan sudut yang mengukur sudut dalam derajat, sedangkan radian adalah satuan sudut yang mengukur sudut dalam satuan panjang busur.
Bagaimana cara mengonversi putaran ke radian?
Kalikan nilai putaran dengan 2π (pi).
Apa saja aplikasi konversi putaran ke radian?
Aplikasi konversi putaran ke radian meliputi perhitungan kecepatan sudut, torsi, dan gerakan benda melingkar.