Pernyataan berikut yang merupakan sifat kubus adalah pertanyaan mendasar dalam geometri. Kubus, sebagai bangun ruang istimewa, memiliki sifat-sifat unik yang membedakannya dari bangun ruang lainnya. Sifat-sifat ini sangat penting untuk dipahami, baik dalam konteks matematika maupun penerapannya dalam kehidupan sehari-hari. Mari kita telusuri lebih dalam tentang definisi, elemen, rumus, dan berbagai penerapannya.
Mempelajari sifat-sifat kubus berarti memahami karakteristiknya yang membedakannya dari bangun ruang lain, seperti balok, prisma, atau limas. Bagaimana sifat-sifat ini terhubung satu sama lain, dan bagaimana pengaruhnya terhadap perhitungan geometri? Kita akan mengupas tuntas hal ini, disertai contoh-contoh praktis dan ilustrasi visual.
Definisi Kubus
Kubus, sebagai bangun ruang tiga dimensi, memiliki karakteristik unik yang membedakannya dari bangun ruang lainnya. Pemahaman mendalam tentang definisi dan sifat-sifatnya sangat penting dalam geometri dan berbagai aplikasi lainnya.
Definisi Matematis Kubus
Kubus didefinisikan sebagai bangun ruang enam sisi yang kongruen berbentuk persegi. Semua rusuknya sama panjang dan semua sudutnya siku-siku. Sifat-sifat ini membentuk karakteristik unik kubus dalam dunia geometri.
Sifat-Sifat Dasar Kubus
Beberapa sifat mendasar kubus yang perlu dipahami meliputi:
- Semua sisi kubus berbentuk persegi yang kongruen (sama bentuk dan ukuran).
- Semua rusuk kubus memiliki panjang yang sama.
- Semua sudut pada kubus adalah sudut siku-siku (90 derajat).
- Setiap sisi kubus berhadapan sejajar dan sama luas.
- Kubus memiliki 8 titik sudut, 12 rusuk, dan 6 sisi.
Perbandingan Kubus dengan Bangun Ruang Lainnya
Untuk memahami keunikan kubus, perbandingan dengan bangun ruang lainnya sangat membantu. Berikut tabel perbandingan:
| Sifat | Kubus | Balok | Prisma Segitiga |
|---|---|---|---|
| Bentuk Sisi | Persegi | Persegi atau persegi panjang | Segitiga atau bentuk lain |
| Panjang Rusuk | Semua sama panjang | Rusuk berlawanan sama panjang | Tergantung pada bentuk alas |
| Sudut | Semua siku-siku | Semua siku-siku (jika semua sisi persegi panjang) | Tergantung pada bentuk alas |
| Jumlah Sisi | 6 | 6 | Tergantung pada bentuk alas |
Perbedaan Kubus dan Bangun Ruang Lainnya
Perbedaan mendasar antara kubus dan bangun ruang lainnya terletak pada kesamaan panjang rusuk dan bentuk sisi yang semuanya persegi. Balok, misalnya, memiliki sisi yang dapat berupa persegi panjang, sementara prisma memiliki sisi alas dan tutup yang dapat berupa berbagai bentuk.
Pernyataan berikut yang merupakan sifat kubus adalah, misalnya, memiliki enam sisi yang sama besar dan berbentuk persegi. Nah, bicara soal bentuk dan permainan, pernahkah terpikir bagaimana jika kita membahas bola dalam permainan bulutangkis? Bola dalam permainan bulutangkis disebut dengan istilah kok, ternyata cukup beragam. Kembali ke sifat kubus, penting untuk diingat bahwa sifat-sifatnya harus konsisten dan terukur untuk memastikan keakuratan dalam geometri.
Begitulah, memahami bentuk-bentuk dasar seperti kubus sangat penting.
Langkah-Langkah Mengidentifikasi Bangun Kubus
Berikut langkah-langkah untuk mengidentifikasi bangun kubus:
- Periksa bentuk sisi: Pastikan semua sisi berbentuk persegi.
- Periksa panjang rusuk: Pastikan semua rusuk memiliki panjang yang sama.
- Periksa sudut: Pastikan semua sudut pada kubus adalah sudut siku-siku.
- Periksa kesamaan sisi: Pastikan semua sisi berhadapan sejajar dan sama luasnya.
- Periksa jumlah sisi, rusuk, dan titik sudut: Pastikan jumlahnya sesuai dengan definisi kubus.
Sifat-Sifat Kubus
Kubus, sebagai bangun ruang istimewa, memiliki sifat-sifat unik yang membedakannya dari bangun ruang lainnya. Pemahaman terhadap sifat-sifat ini penting untuk mengaplikasikan konsep geometri dalam berbagai bidang, mulai dari perhitungan volume dan luas permukaan hingga desain dan konstruksi.
Identifikasi Sifat-Sifat Kubus
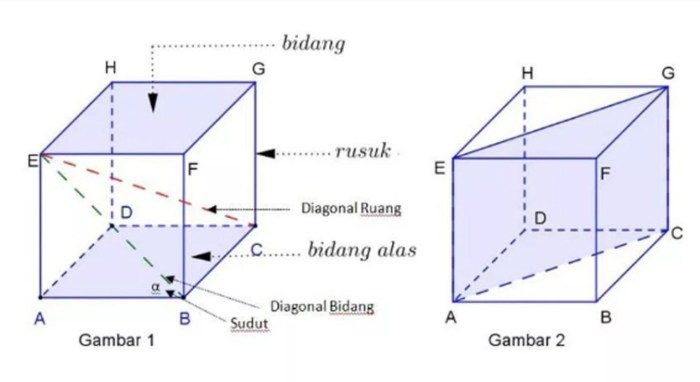
Kubus memiliki enam sisi yang kongruen (sama bentuk dan ukuran). Setiap sisi berbentuk persegi. Diagonal ruang, yang menghubungkan dua titik sudut yang tidak berimpit pada sisi yang sama, juga memiliki panjang yang sama.
Penjelasan Sifat-Sifat Kubus
- Sisi-sisi Kongruen: Semua sisi kubus memiliki bentuk dan ukuran yang sama, yaitu persegi.
- Sudut-sudut siku-siku: Semua sudut yang terbentuk pada pertemuan antar sisi kubus adalah sudut siku-siku (90 derajat).
- Rusuk-rusuk sama panjang: Panjang semua rusuk pada kubus sama.
- Diagonal ruang sama panjang: Semua diagonal ruang kubus memiliki panjang yang sama.
- Diagonal bidang sama panjang: Semua diagonal bidang pada sisi-sisi kubus memiliki panjang yang sama. Panjang diagonal bidang pada kubus dengan rusuk ‘s’ adalah s√2.
- Bidang-bidang sejajar: Setiap sisi kubus sejajar dengan sisi yang berlawanan.
Tabel Sifat-Sifat Kubus dan Contohnya
| Sifat | Penjelasan | Contoh |
|---|---|---|
| Sisi Kongruen | Semua sisi memiliki bentuk dan ukuran yang sama. | Keenam sisi dadu standar berbentuk persegi dan ukurannya sama. |
| Sudut siku-siku | Semua sudut pertemuan antar sisi adalah 90 derajat. | Pertemuan antar dinding dan lantai pada ruangan yang berbentuk kubus. |
| Rusuk sama panjang | Panjang setiap rusuk pada kubus sama. | Kotak kardus yang berbentuk kubus, setiap sisinya memiliki panjang yang sama. |
| Diagonal ruang sama panjang | Semua diagonal ruang memiliki panjang yang sama. | Diagonal pada kerangka balok. |
| Diagonal bidang sama panjang | Diagonal bidang pada sisi kubus memiliki panjang yang sama. | Diagonal pada kotak mainan. |
| Bidang sejajar | Setiap sisi kubus sejajar dengan sisi yang berlawanan. | Lantai dan atap sebuah ruangan yang berbentuk kubus. |
Hubungan Antar Sifat-Sifat Kubus
Sifat-sifat kubus saling terkait. Misalnya, sifat sisi-sisi yang kongruen dan sudut-sudut siku-siku menentukan bentuk dasar kubus sebagai bangun ruang yang teratur. Sifat-sifat ini juga memengaruhi perhitungan volume dan luas permukaan kubus.
Perbedaan dengan Bangun Ruang Lain
Bangun ruang lain seperti balok, prisma, atau limas memiliki sifat-sifat yang berbeda. Balok memiliki sisi-sisi yang berpasangan dan kongruen, tetapi tidak semua sisinya persegi. Prisma dan limas memiliki sisi-sisi yang lebih kompleks, dan tidak memiliki sifat-sifat sudut siku-siku dan rusuk sama panjang yang dimiliki kubus.
Implikasi dalam Penerapan
Pemahaman sifat-sifat kubus sangat penting dalam berbagai bidang. Dalam arsitektur, kubus menjadi dasar bagi desain bangunan. Dalam matematika, sifat-sifat kubus digunakan dalam perhitungan geometri dan penyelesaian masalah terkait volume, luas permukaan, dan diagonal. Contohnya dalam perhitungan volume material yang dibentuk oleh kubus.
Elemen Kubus
Kubus, sebagai bentuk geometri tiga dimensi yang teratur, dibangun dari beberapa elemen dasar. Memahami elemen-elemen ini akan membuka wawasan kita tentang struktur dan karakteristiknya. Mari kita telusuri lebih dalam bagaimana elemen-elemen ini saling terkait membentuk suatu kubus.
Pernyataan berikut yang merupakan sifat kubus adalah, misalnya, memiliki enam sisi persegi. Nah, berbicara tentang bentuk dan gerakan, senam irama akan bermanfaat apabila dilakukan dengan konsentrasi dan koordinasi yang baik. Bayangkan, gerakan-gerakan yang terstruktur dan indah dalam senam irama, itu mengingatkan kita pada simetri dan kesempurnaan sisi-sisi kubus yang sama. Jadi, memahami sifat kubus, pada dasarnya, juga mengarah pada pemahaman pentingnya harmonisasi dalam berbagai aspek kehidupan.
Elemen Pembentuk Kubus
Kubus tersusun dari sisi, rusuk, dan titik sudut. Ketiga elemen ini saling berkaitan dan menentukan bentuk kubus secara keseluruhan. Pemahaman mendalam tentang hubungan antar elemen ini akan memperjelas konsep geometri kubus.
Sisi Kubus
Sisi kubus adalah bidang datar yang membentuk permukaan kubus. Kubus memiliki enam sisi yang kongruen (sama ukuran dan bentuk). Setiap sisi merupakan persegi yang sama ukurannya. Bayangkan setiap sisi sebagai permukaan persegi yang membentuk kotak tiga dimensi.
- Setiap sisi berperan dalam menentukan luas permukaan kubus.
- Contoh: Dalam sebuah kotak kardus berbentuk kubus, setiap permukaan kotak tersebut adalah sisi kubus. Ukuran setiap sisi dapat diukur dan dihitung luasnya.
Rusuk Kubus
Rusuk kubus adalah garis lurus yang menghubungkan dua titik sudut berdekatan. Kubus memiliki 12 rusuk, dengan panjang yang sama pada setiap rusuknya. Rusuk-rusuk ini membentuk kerangka utama kubus.
- Rusuk-rusuk tersebut menentukan panjang sisi kubus.
- Contoh: Pada sebuah mainan balok kayu berbentuk kubus, setiap garis tepi yang menghubungkan sisi-sisi kotak tersebut adalah rusuk kubus.
Titik Sudut Kubus
Titik sudut kubus adalah titik pertemuan tiga rusuk. Kubus memiliki 8 titik sudut. Titik-titik sudut ini menjadi penentu bentuk keseluruhan kubus.
- Titik-titik sudut berperan penting dalam menentukan volume dan ukuran kubus.
- Contoh: Pada model kubus yang terbuat dari kawat, setiap titik pertemuan kawat merupakan titik sudut kubus.
Hubungan Antar Elemen
Sisi, rusuk, dan titik sudut saling berkaitan erat dalam membentuk struktur kubus. Rusuk menghubungkan dua titik sudut dan membentuk sisi-sisi kubus. Setiap sisi terdiri dari empat rusuk yang bertemu di empat titik sudut.
| Elemen | Hubungan dengan Elemen Lain | Contoh |
|---|---|---|
| Sisi | Terdiri dari 4 rusuk dan 4 titik sudut | Permukaan persegi pada kotak kado |
| Rusuk | Menghubungkan dua titik sudut dan membentuk sisi | Garis tepi kotak |
| Titik Sudut | Pertemuan tiga rusuk dan penentu bentuk kubus | Titik pertemuan tiga rusuk pada sudut kotak |
Urutan Elemen Pembentuk Kubus
Urutan elemen pembentuk kubus dari yang paling mendasar hingga kompleks dimulai dari titik sudut, dilanjutkan rusuk, dan diakhiri dengan sisi. Titik sudut merupakan fondasi, rusuk membentuk kerangka, dan sisi membentuk permukaan kubus.
- Titik Sudut: Titik pertemuan tiga rusuk yang menjadi dasar pembentukan.
- Rusuk: Garis lurus yang menghubungkan titik-titik sudut, membentuk kerangka kubus.
- Sisi: Bidang datar yang dibentuk oleh empat rusuk dan empat titik sudut, membentuk permukaan kubus.
Rumus dan Perhitungan
Mengetahui rumus dan cara menghitung luas permukaan serta volume kubus sangat penting dalam geometri. Pemahaman yang mendalam akan memudahkan kita dalam berbagai aplikasi, dari perhitungan volume material bangunan hingga pemahaman konsep matematika dasar.
Rumus Luas Permukaan
Luas permukaan kubus dihitung dengan memperhatikan jumlah semua sisi persegi yang menyusunnya. Kubus memiliki enam sisi yang sama luasnya. Rumus yang digunakan adalah mengalikan luas satu sisi dengan enam.
Luas Permukaan = 6 x (sisi2)
Dimana ‘s’ adalah panjang sisi kubus. Perhitungan ini didasarkan pada sifat dasar kubus yang memiliki sisi-sisi yang kongruen.
Rumus Volume
Volume kubus dihitung dengan memperhatikan isi ruang yang ditempati oleh kubus. Rumus volume kubus didapat dengan mengalikan panjang sisi tiga kali.
Volume = sisi3
Rumus ini merepresentasikan hubungan linier antara panjang sisi dan volume yang ditempati.
Contoh Soal dan Perhitungan
Untuk memperjelas penerapan rumus, berikut beberapa contoh soal dan perhitungan:
- Contoh 1: Sebuah kubus memiliki sisi sepanjang 5 cm. Hitung luas permukaan dan volumenya.
- Solusi:
- Luas Permukaan: Luas Permukaan = 6 x (5 cm) 2 = 6 x 25 cm 2 = 150 cm 2
- Volume: Volume = (5 cm) 3 = 125 cm 3
Contoh-contoh di atas memperlihatkan bagaimana rumus-rumus tersebut digunakan dalam praktik.
Tabel Rumus dan Contoh
| Rumus | Penjelasan | Contoh |
|---|---|---|
| Luas Permukaan = 6 x (sisi2) | Rumus untuk menghitung total luas semua sisi kubus. | Jika sisi = 3 cm, maka Luas Permukaan = 6 x (3 cm)2 = 54 cm2 |
| Volume = sisi3 | Rumus untuk menghitung volume kubus. | Jika sisi = 4 cm, maka Volume = (4 cm)3 = 64 cm3 |
Faktor-faktor yang Memengaruhi Perhitungan
Faktor utama yang memengaruhi perhitungan luas permukaan dan volume kubus adalah panjang sisi (s). Semakin panjang sisi, semakin besar luas permukaan dan volumenya.
Selain panjang sisi, tidak ada faktor lain yang memengaruhi perhitungan dasar ini. Perhitungan ini bersifat langsung dan deterministik, tidak ada faktor eksternal yang berpengaruh.
Contoh Penerapan Kubus dalam Kehidupan Sehari-hari
Source: ruangguru.com
Kubus, dengan sifat-sifatnya yang simetris dan konsisten, ternyata memiliki peran yang tak terduga dalam berbagai aspek kehidupan kita. Dari yang terkecil hingga yang terbesar, kita dapat menemukan aplikasi kubus yang menarik dan bermanfaat. Mari kita telusuri contoh-contoh nyata penerapannya.
Kotak Kardus dan Pengemasan
Kotak kardus yang kita temui sehari-hari, seperti kotak sepatu, kotak pizza, atau bahkan kotak kado, seringkali berbentuk kubus atau balok. Bentuk kubus dipilih karena efisiensi. Sifat-sifat kubus, seperti sisi-sisi yang sama panjang dan sudut siku-siku, membuat kotak-kotak ini mudah dibentuk dan ditumpuk. Hal ini memungkinkan pengemasan barang dengan optimal, menghemat ruang dan biaya.
- Efisiensi ruang: Bentuk kubus memungkinkan penataan barang yang kompak dan efektif, meminimalkan ruang kosong dalam kemasan.
- Kestabilan: Sudut siku-siku kubus memberikan kestabilan pada kotak, mencegah barang di dalamnya bergeser atau jatuh.
- Kemudahan penanganan: Bentuk yang tegas dan sudut yang tepat membuat kotak kubus mudah diangkat, dipindahkan, dan disimpan.
Bangunan dan Arsitektur
Meskipun tidak selalu tampak sebagai bentuk kubus murni, banyak bangunan dan elemen arsitektur yang terinspirasi oleh geometri kubus. Bentuk-bentuk kubus dapat ditemukan dalam desain rumah, gedung perkantoran, bahkan dalam detail-detail kecil. Sifat-sifatnya yang stabil dan mudah diinterpretasi secara visual menjadikannya pilihan menarik bagi para arsitek.
- Rumah-rumah bergaya minimalis: Seringkali menggunakan bentuk kubus untuk desain dinding, atap, dan bangunannya secara keseluruhan.
- Elemen dekoratif: Bentuk kubus dapat diimplementasikan dalam berbagai ornamen atau dekorasi bangunan, memberikan kesan modern dan tegas.
- Struktur bangunan: Konstruksi kolom dan dinding yang tegak lurus dan beraturan dapat dianalogikan dengan geometri kubus yang kuat dan kokoh.
Permainan dan Hiburan
- Dadu: Bentuk kubus yang standar digunakan dalam banyak permainan dadu. Sifat sisi-sisi yang sama panjang dan jumlah titik yang beraturan dalam dadu memungkinkan permainan yang adil dan transparan.
- Permainan papan: Beberapa permainan papan memiliki elemen kubus dalam bentuk pion atau komponen lainnya. Bentuk kubus membantu dalam penempatan dan pergerakan objek dalam permainan.
- Bangunan Lego: Kubus adalah blok dasar dalam konstruksi Lego. Sifat-sifatnya yang stabil dan dapat dikombinasikan memungkinkan anak-anak membangun berbagai macam bentuk dan struktur.
Ilustrasi gambar dapat dibayangkan sebagai berbagai macam kotak kardus, desain rumah minimalis, dadu, dan blok-blok Lego yang tersusun dalam berbagai bentuk.
Industri Manufaktur
Industri manufaktur memanfaatkan bentuk kubus untuk efisiensi dan penyusunan produk. Sifat kubus yang mudah diukur dan disusun memungkinkan untuk pengemasan dan pengiriman produk secara optimal.
- Produksi komponen elektronik: Bentuk kubus dapat diterapkan pada casing perangkat elektronik untuk memberikan kestabilan dan tampilan yang modern.
- Pengemasan produk: Kotak kemasan produk, baik makanan atau barang lainnya, seringkali berbentuk kubus atau balok untuk efisiensi ruang dan kestabilan produk di dalam.
Perbedaan Kubus dengan Bangun Ruang Lain
Kubus, sebagai bangun ruang istimewa, memiliki karakteristik unik yang membedakannya dari bangun ruang lainnya. Keunikan ini tak hanya terletak pada bentuknya, tetapi juga memengaruhi perhitungan-perhitungan yang terkait. Mari kita telusuri perbedaan-perbedaannya dengan balok, prisma, limas, dan bangun ruang lainnya.
Perbedaan Kubus dengan Balok
Perbedaan utama kubus dengan balok terletak pada sisi-sisinya. Kubus memiliki enam sisi yang sama dan kongruen (bentuk dan ukuran sama), sedangkan balok memiliki enam sisi yang tidak semuanya kongruen. Setiap sisi kubus berbentuk persegi, sedangkan balok memiliki sisi-sisi yang berbentuk persegi atau persegi panjang. Perbedaan ini berdampak langsung pada rumus volume dan luas permukaan. Volume kubus dihitung dengan sisi pangkat tiga, berbeda dengan balok yang menggunakan panjang, lebar, dan tinggi.
Perbedaan Kubus dengan Prisma
Kubus dan prisma sama-sama memiliki sisi-sisi datar. Namun, kubus memiliki sisi-sisi yang berbentuk persegi, sedangkan prisma dapat memiliki berbagai macam bentuk poligon pada sisi-sisinya. Prisma juga memiliki dua alas yang sejajar dan kongruen. Kubus, dengan sisi-sisinya yang sama, merupakan kasus khusus dari prisma dengan alas persegi.
Perbedaan Kubus dengan Limas
Kubus memiliki enam sisi persegi, sedangkan limas memiliki alas berbentuk poligon dan sisi-sisi tegak berbentuk segitiga. Kubus tidak memiliki puncak atau titik puncak, berbeda dengan limas yang memiliki puncak tunggal di atas alasnya. Hal ini juga mempengaruhi perhitungan luas permukaan dan volume, yang memiliki rumus yang berbeda secara signifikan.
Perbedaan Kubus dengan Bangun Ruang Lainnya
Perbedaan kubus dengan bangun ruang lainnya terletak pada simetri dan sifat-sifat geometriknya. Kubus memiliki simetri rotasi dan simetri cermin yang lebih kompleks dibandingkan bangun ruang lainnya. Misalnya, kubus memiliki 9 bidang simetri, sementara bangun ruang lainnya mungkin memiliki jumlah simetri yang lebih sedikit atau bahkan tidak memiliki simetri sama sekali.
Tabel Perbandingan
| Karakteristik | Kubus | Balok | Prisma | Limas |
|---|---|---|---|---|
| Bentuk Sisi | Persegi (semua sisi kongruen) | Persegi atau persegi panjang (sisi-sisi tidak semuanya kongruen) | Poligon (dapat beragam) | Segitiga dan poligon (alas) |
| Sisi | 6 sisi | 6 sisi | Dua alas sejajar dan sisi-sisi tegak | Satu alas dan sisi-sisi tegak berbentuk segitiga |
| Puncak | Tidak ada | Tidak ada | Tidak ada | Ada |
| Rumus Volume | s3 | p x l x t | Luas alas x tinggi | 1/3 x Luas alas x tinggi |
Ilustrasi Perbedaan
Kubus dapat divisualisasikan sebagai kotak yang sempurna, dengan semua sisinya berukuran sama. Balok dapat dibayangkan sebagai kotak yang tidak semua sisinya sama panjang. Prisma dapat berbentuk segitiga, persegi, atau poligon lainnya, dengan dua alas yang sejajar dan kongruen. Limas memiliki alas berbentuk segitiga, persegi, atau poligon lainnya, dan sisi-sisi tegak yang bertemu di satu titik puncak.
Dampak Perbedaan pada Perhitungan
Perbedaan dalam bentuk dan sifat bangun ruang ini berdampak langsung pada rumus perhitungan volume dan luas permukaan. Rumus kubus yang sederhana (s 3) berbeda dengan rumus balok (p x l x t) dan rumus bangun ruang lainnya. Ini menunjukkan betapa pentingnya memahami bentuk dan sifat bangun ruang untuk menghitung ukurannya dengan benar.
Hubungan Sifat Kubus dengan Geometri
Kubus, sebagai bangun ruang istimewa, memiliki keterkaitan erat dengan berbagai konsep geometri. Sifat-sifatnya yang kaku dan simetris menjadi fondasi penting dalam memahami konsep-konsep geometri yang lebih kompleks, dari dasar hingga aplikasi praktis. Pemahaman ini memungkinkan kita untuk melihat keterkaitan yang mendalam antara bangun ruang sederhana dan prinsip-prinsip geometri.
Hubungan Sifat-Sifat dengan Konsep Geometri Dasar
Sifat-sifat kubus, seperti sisi-sisi yang sama panjang, sudut-sudut yang siku-siku, dan rusuk-rusuk yang sejajar, secara langsung merepresentasikan konsep-konsep dasar geometri. Misalnya, kesamaan panjang sisi-sisi kubus merupakan aplikasi dari konsep kesebangunan. Sudut siku-siku pada setiap sudut kubus adalah representasi dari sudut tegak lurus dalam geometri. Sejajarnya rusuk-rusuk kubus menjelaskan konsep kesebangunan dan kesejajaran dalam ruang tiga dimensi.
Pernyataan berikut yang merupakan sifat kubus adalah, misalnya, memiliki enam sisi yang sama luasnya. Namun, untuk merencanakan proyek yang baik, kita juga perlu mempertimbangkan anggaran biaya dalam proposal berisi rincian yang komprehensif. Rincian anggaran biaya dalam proposal berisi merupakan elemen krusial untuk memastikan kelancaran proyek dan menghindari masalah di kemudian hari. Lalu, kembali ke sifat kubus, penting untuk memahami bahwa sisi-sisi tersebut juga memiliki sudut siku-siku, yang merupakan karakteristik penting lainnya dari bentuk geometris ini.
Penerapan dalam Teorema Geometri
Sifat-sifat kubus menjadi dasar dalam beberapa teorema geometri. Contohnya, dalam menghitung volume dan luas permukaan kubus, kita memanfaatkan teorema dasar geometri ruang. Perhitungan ini melibatkan rumus-rumus yang didasarkan pada sifat-sifat kubus. Lebih lanjut, teorema Pythagoras dapat diaplikasikan pada diagonal ruang kubus untuk menghitung panjangnya.
Konsep Geometri Terkait Kubus
- Kesebangunan: Sifat kesebangunan sisi-sisi kubus, serta konsep kesebangunan dalam bangun ruang lain yang terkait dengan kubus, dapat dipelajari lebih lanjut.
- Ketegaklurusan: Sudut siku-siku pada setiap sudut kubus merupakan representasi dari konsep ketegaklurusan yang fundamental dalam geometri.
- Kesejajaran: Sifat kesejajaran rusuk-rusuk kubus menggambarkan konsep kesejajaran dalam ruang tiga dimensi.
- Volume dan Luas Permukaan: Rumus volume dan luas permukaan kubus merupakan aplikasi langsung dari sifat-sifatnya, yang dapat diaplikasikan pada berbagai permasalahan geometri.
- Diagonal Ruang: Perhitungan panjang diagonal ruang kubus melibatkan teorema Pythagoras dan sifat-sifat kubus yang telah dibahas.
Hubungan dengan Konsep Geometri yang Lebih Kompleks
Sifat-sifat kubus, yang sederhana namun fundamental, menjadi fondasi untuk memahami konsep geometri yang lebih kompleks. Misalnya, pemahaman tentang kubus dapat membantu dalam mempelajari sifat-sifat bangun ruang lainnya, seperti prisma dan balok. Selain itu, prinsip-prinsip geometri yang dibangun dari sifat-sifat kubus menjadi penting dalam aplikasi-aplikasi geometri yang lebih canggih, seperti dalam rekayasa dan arsitektur.
Representasi Visual Kubus
Source: cerdika.com
Memahami bentuk tiga dimensi seperti kubus bisa jadi lebih mudah dengan representasi visual yang tepat. Ilustrasi yang baik dapat membantu kita membayangkan bagaimana sebuah kubus terlihat dari berbagai sudut pandang dan bagaimana ia dapat dipotong atau dibentuk.
Berbagai Perspektif Kubus
Memahami bentuk kubus secara keseluruhan membutuhkan pemahaman dari berbagai sudut pandang. Ilustrasi kubus dari sisi depan, samping, dan atas akan memberikan gambaran yang lebih utuh.
- Tampak Depan: Ilustrasi ini menampilkan kubus seperti yang kita lihat dari arah depannya. Kita akan melihat enam persegi, dengan empat persegi membentuk sisi-sisi yang terlihat, dan dua persegi lagi sebagai bagian belakang yang tersembunyi. Bentuknya jelas persegi empat dengan sudut siku-siku.
- Tampak Samping: Ilustrasi ini menampilkan kubus dari sisi samping. Di sini kita akan melihat empat persegi, dua persegi membentuk sisi-sisi yang terlihat dan dua persegi lainnya sebagai bagian belakang yang tersembunyi. Kembali, bentuk persegi empat dengan sudut siku-siku menjadi ciri khasnya.
- Tampak Atas: Ilustrasi ini menampilkan kubus dari atas. Kita akan melihat sebuah persegi dengan sisi-sisi yang tersusun secara tegak lurus.
Pemotongan Kubus
Pemahaman tentang bagaimana kubus dapat dipotong akan memperkaya pemahaman kita tentang bentuknya. Ilustrasi pemotongan akan menunjukkan bagaimana bidang potongan mempengaruhi bentuk yang dihasilkan.
- Potongan Melintang: Ilustrasi pemotongan kubus secara melintang akan menghasilkan potongan berbentuk persegi. Potongan ini akan terlihat sebagai persegi yang sama dengan sisi kubus.
- Potongan Miring: Ilustrasi pemotongan miring akan menghasilkan potongan berbentuk trapesium atau segiempat tak beraturan. Bentuk potongan akan tergantung pada sudut kemiringan bidang potongan.
Visualisasi 3D Kubus
Visualisasi 3D kubus memungkinkan kita untuk melihat bentuk kubus secara penuh dalam ruang tiga dimensi. Ini sangat membantu untuk memahami hubungan antara berbagai sisi dan sudut kubus.
Bayangkan sebuah kotak yang semua sisinya berbentuk persegi yang sama dan semua sudutnya siku-siku. Ilustrasi 3D akan menunjukkan bahwa setiap sisi kubus sejajar dengan sisi-sisi lainnya dan saling tegak lurus. Ini penting untuk memahami karakteristik geometri kubus.
Ilustrasi dan Pemahaman Kubus
Ilustrasi yang tepat dapat menjadi kunci untuk memahami kompleksitas kubus. Dengan melihat berbagai perspektif dan pemotongan, kita dapat membangun pemahaman yang lebih mendalam tentang bentuk dan sifatnya.
Misalnya, gambaran kubus dari berbagai sudut pandang akan membantu kita memahami bahwa meskipun bentuknya terlihat berbeda, struktur dasarnya tetap sama, yaitu enam persegi yang saling terhubung.
Variasi dan Modifikasi Kubus
Kubus, sebagai bangun ruang dasar, memiliki sifat-sifat yang fundamental. Namun, bentuknya dapat dimodifikasi dengan berbagai cara, menciptakan variasi yang menarik dan memengaruhi karakteristiknya. Modifikasi ini tidak hanya sekadar mengubah tampilan, tetapi juga berdampak pada sifat-sifat geometriknya.
Bentuk-Bentuk Kubus yang Termodifikasi
Beberapa modifikasi kubus yang umum ditemui meliputi kubus terpotong, kubus berlubang, dan kombinasi keduanya. Modifikasi ini menciptakan bentuk-bentuk baru yang tetap mempertahankan beberapa sifat dasar kubus, namun juga memiliki karakteristik unik tersendiri.
Kubus Terpotong, Pernyataan berikut yang merupakan sifat kubus adalah
Kubus terpotong dihasilkan dengan memotong bagian-bagian tertentu dari kubus asli. Potongan dapat dilakukan pada sisi-sisi kubus, membentuk penampang yang unik. Misalnya, memotong sudut-sudut kubus akan menghasilkan bentuk yang lebih melengkung. Bentuk-bentuk potongan ini dapat menghasilkan bangun ruang baru yang tidak lagi memenuhi definisi kubus, namun masih memiliki keterkaitan geometrik dengan kubus awal.
Kubus Berlubang
Kubus berlubang melibatkan pengurangan volume kubus asli dengan membuat lubang di dalamnya. Lubang tersebut dapat berbentuk bulat, persegi panjang, atau bahkan bentuk lainnya. Lubang ini dapat berada di tengah kubus, di sisi-sisi, atau kombinasi keduanya. Hal ini akan memengaruhi volume dan luas permukaan kubus secara signifikan, serta merubah distribusi massanya.
Tabel Perbandingan
| Karakteristik | Kubus Biasa | Kubus Terpotong | Kubus Berlubang |
|---|---|---|---|
| Jumlah Sisi | 6 | Lebih dari 6 (tergantung bentuk potongan) | 6 |
| Jumlah Titik Sudut | 8 | Lebih dari 8 (tergantung bentuk potongan) | 8 |
| Volume | s3 | Berubah tergantung bentuk potongan | Berubah tergantung ukuran lubang |
| Luas Permukaan | 6s2 | Berubah tergantung bentuk potongan | Berubah tergantung ukuran lubang |
Penerapan Kubus Termodifikasi
Kubus termodifikasi, seperti kubus berlubang, memiliki aplikasi dalam berbagai bidang, termasuk desain arsitektur dan industri. Contohnya, desain interior dapat memanfaatkan kubus terpotong untuk menciptakan elemen dekoratif yang unik. Sedangkan dalam industri manufaktur, kubus berlubang dapat digunakan untuk mengoptimalkan penggunaan material dan mengurangi berat.
Penerapan dalam Bidang Lain: Pernyataan Berikut Yang Merupakan Sifat Kubus Adalah
Kubus, dengan bentuknya yang sederhana dan simetris, memiliki aplikasi yang luas di berbagai bidang. Dari arsitektur hingga teknik, dan bahkan seni, kita dapat menemukan jejak-jejak keberadaan kubus dalam berbagai karya dan rancangan. Kemampuannya untuk membentuk pola, menciptakan volume, dan menyediakan struktur yang kokoh menjadikan kubus sebagai elemen penting dalam banyak desain.
Penerapan dalam Arsitektur
Bentuk kubus yang fundamental sering diadopsi dalam perancangan bangunan. Bentuk kubus yang sederhana dan mudah dipahami sering digunakan untuk menciptakan ruang-ruang yang fungsional dan efisien. Bangunan-bangunan yang berbentuk kubus dapat ditemukan dalam berbagai konteks, mulai dari rumah tinggal hingga gedung perkantoran. Bentuknya yang teratur memungkinkan perancangan yang lebih mudah dan dapat meminimalkan penggunaan material.
- Contoh Desain Rumah: Rumah dengan bentuk kubus yang sederhana, namun dengan variasi atap dan penambahan elemen dekoratif dapat menciptakan rumah yang modern dan menarik. Penerapan pencahayaan dan ventilasi alami menjadi penting dalam desain rumah kubus untuk menciptakan kenyamanan bagi penghuninya.
- Gedung Perkantoran: Bentuk kubus yang terstruktur dan teratur dapat diaplikasikan untuk menciptakan gedung perkantoran yang efisien dan modern. Penggunaan material yang tepat dan penataan ruang yang optimal akan menciptakan suasana kerja yang nyaman dan produktif.
- Bangunan Publik: Dalam perancangan bangunan publik, seperti sekolah atau pusat perbelanjaan, bentuk kubus dapat diaplikasikan untuk menciptakan ruang-ruang yang luas dan fleksibel. Kejelasan struktur dan pengaturan ruang dapat memudahkan pengelolaan dan penggunaan bangunan.
Penerapan dalam Teknik
Dalam teknik sipil dan mesin, kubus sering menjadi dasar untuk perancangan dan analisis struktur. Bentuknya yang stabil dan teratur memungkinkan perhitungan yang lebih mudah dan akurat dalam hal beban, kekuatan, dan stabilitas. Kemampuan untuk menggabungkan beberapa kubus juga memungkinkan konstruksi yang lebih kompleks dan inovatif.
Pernyataan berikut yang merupakan sifat kubus adalah, misalnya, memiliki enam sisi yang sama. Namun, untuk memahami bagaimana sifat-sifat geometris ini terbentuk, kita perlu melihat lebih jauh. Sosiologi, yang mempelajari aspek utama interaksi antara manusia dan lingkungan sosialnya aspek utama yang dipelajari oleh sosiologi adalah interaksi antara , juga menawarkan perspektif unik untuk menganalisis struktur dan hubungan yang tercipta dalam bentuk-bentuk geometri seperti kubus.
Pada akhirnya, pemahaman tentang sifat kubus, seperti sisi-sisi yang sama dan sudut siku-siku, tetap berakar pada konsep-konsep dasar matematika dan geometri.
- Konstruksi Bangunan: Kubus menjadi dasar untuk analisis struktur bangunan. Dengan memahami sifat-sifat kubus, para insinyur dapat menentukan kekuatan dan stabilitas bangunan di bawah berbagai kondisi beban.
- Rancang Bangun Mesin: Dalam desain mesin, bentuk kubus sering digunakan sebagai blok dasar untuk membentuk komponen yang lebih kompleks. Contohnya, mesin yang memiliki banyak bagian kotak dapat dianggap sebagai gabungan dari banyak kubus.
- Analisis Material: Sifat-sifat kubus, seperti volume dan luas permukaan, digunakan untuk menganalisis perilaku material di bawah tekanan atau tegangan. Penggunaan kubus sebagai model dapat membantu dalam prediksi dan perencanaan.
Penerapan dalam Desain
Dalam desain grafis dan industri, kubus dapat digunakan untuk menciptakan komposisi visual yang menarik dan terstruktur. Bentuknya yang sederhana dan simetris dapat menjadi elemen dasar dalam menciptakan pola dan tekstur. Bentuk kubus dapat digunakan untuk memperkuat kesan modernitas dan minimalisme dalam desain.
- Desain Produk: Bentuk kubus sering digunakan dalam desain produk untuk menciptakan kesan yang modern dan fungsional. Penggunaan material dan warna yang tepat dapat membuat produk lebih menarik.
- Desain Grafis: Dalam desain grafis, kubus dapat digunakan untuk menciptakan pola dan tekstur yang menarik. Penggunaan warna dan ukuran yang tepat dapat menciptakan efek visual yang menarik.
- Desain Interior: Kubus dapat digunakan sebagai elemen dalam desain interior untuk menciptakan kesan ruang yang terstruktur dan terorganisir. Penggunaan pencahayaan dan material yang tepat dapat membuat ruang lebih menarik.
Terakhir
Kesimpulannya, memahami pernyataan berikut yang merupakan sifat kubus adalah kunci untuk menguasai konsep geometri ruang. Dari definisi dasar hingga penerapannya dalam berbagai bidang, kubus menghadirkan kompleksitas yang menarik. Pemahaman yang mendalam tentang sifat-sifat kubus akan membuka pintu untuk memahami konsep geometri yang lebih kompleks dan aplikasinya di dunia nyata. Semoga pembahasan ini memberikan wawasan baru dan bermanfaat.
Tanya Jawab (Q&A)
Apakah semua persegi panjang dapat membentuk kubus?
Tidak. Untuk membentuk kubus, persegi panjang harus memiliki sisi-sisi yang sama panjang dan sudut siku-siku pada semua sisinya.
Bagaimana cara membedakan kubus dengan balok?
Kubus memiliki semua sisi berbentuk persegi yang sama luasnya, sedangkan balok memiliki sisi-sisi yang berbentuk persegi panjang yang tidak semuanya sama luasnya.
Apakah semua sisi kubus memiliki panjang yang sama?
Ya, semua sisi kubus memiliki panjang yang sama.