Soal akar pangkat 3 seringkali menjadi tantangan bagi banyak siswa. Bagaimana kita memahami dan menguasai konsep ini? Mari kita telusuri lebih dalam tentang akar pangkat 3, dari definisi hingga penerapannya dalam kehidupan sehari-hari.
Akar pangkat 3 adalah kebalikan dari perpangkatan dengan pangkat tiga. Memahami hubungan ini akan sangat membantu dalam memecahkan soal-soal yang melibatkan akar pangkat 3. Kita akan melihat berbagai contoh, mulai dari bilangan bulat hingga desimal, serta bagaimana menyelesaikannya dengan berbagai metode.
Definisi Akar Pangkat 3
Akar pangkat tiga, atau sering disebut akar kubik, merupakan operasi matematika yang berlawanan dengan perpangkatan dengan eksponen 3. Konsep ini sangat penting dalam berbagai bidang, dari matematika dasar hingga aplikasi sains dan teknik.
Definisi Singkat dan Jelas
Akar pangkat tiga dari suatu bilangan adalah bilangan yang, jika dipangkatkan tiga, hasilnya sama dengan bilangan tersebut. Misalnya, akar pangkat tiga dari 8 adalah 2, karena 2 3 = 8.
Hubungan dengan Perpangkatan
Akar pangkat tiga merupakan kebalikan dari perpangkatan dengan eksponen 3. Jika kita memiliki x3 = y, maka akar pangkat tiga dari y adalah x. Ini menggambarkan hubungan timbal balik antara kedua operasi tersebut.
Perbandingan dengan Akar Pangkat 2, Soal akar pangkat 3
Berikut tabel yang membandingkan akar pangkat 3 dengan akar pangkat 2:
| Karakteristik | Akar Pangkat 2 | Akar Pangkat 3 |
|---|---|---|
| Definisi | Bilangan yang, jika dikuadratkan, hasilnya sama dengan bilangan tersebut. | Bilangan yang, jika dipangkatkan tiga, hasilnya sama dengan bilangan tersebut. |
| Notasi | √x | 3√x |
| Contoh | √9 = 3 (karena 32 = 9) | 3√27 = 3 (karena 33 = 27) |
| Sifat Dasar | Berhubungan dengan kuadrat sempurna. | Berhubungan dengan kubus sempurna. |
Tabel di atas memperlihatkan perbedaan notasi dan definisi yang membedakan kedua jenis akar ini. Meskipun keduanya merupakan operasi invers dari perpangkatan, basisnya berbeda, yang berdampak pada sifat-sifat dan penerapannya.
Cara Menghitung Akar Pangkat 3
Mengetahui cara menghitung akar pangkat tiga sangat penting dalam berbagai bidang, dari matematika dasar hingga aplikasi sains dan teknik. Metode-metode yang akan dibahas di sini akan membantu Anda memahami proses perhitungan dengan lebih baik, mulai dari cara manual hingga menggunakan alat bantu.
Metode Pemfaktoran
Metode pemfaktoran efektif untuk bilangan-bilangan yang memiliki faktor pangkat tiga yang jelas. Kita perlu menguraikan bilangan tersebut menjadi faktor-faktornya dan mencari faktor-faktor yang berulang tiga kali. Misalnya, untuk menghitung akar pangkat tiga dari 27, kita bisa memfaktorkan 27 menjadi 3 x 3 x 3. Maka, akar pangkat tiga dari 27 adalah 3.
Namun, metode ini memiliki keterbatasan. Ia hanya efektif untuk bilangan yang memiliki faktor pangkat tiga yang mudah diidentifikasi. Untuk bilangan yang lebih kompleks, metode lain seperti metode perkiraan mungkin lebih praktis.
Metode Perkiraan
Metode perkiraan, terutama untuk bilangan yang tidak memiliki faktor pangkat tiga yang mudah ditemukan, melibatkan pendekatan bertahap. Kita perlu mencari bilangan yang, jika dipangkatkan tiga, mendekati bilangan yang dicari. Misalnya, untuk menghitung akar pangkat tiga dari 100, kita perlu mencari bilangan yang jika dipangkatkan tiga hasilnya mendekati 100. Kita tahu bahwa 4 3 = 64 dan 5 3 = 125.
Menghitung akar pangkat 3, sejatinya, adalah tentang menemukan angka yang, jika dikalikan dengan dirinya sendiri sebanyak tiga kali, menghasilkan angka yang kita cari. Bayangkan, itu seperti mencari kecepatan ekstrem untuk menempuh jarak tertentu. Seperti halnya kemampuan menempuh jarak dalam waktu yang sesingkat singkatnya disebut , akar pangkat 3 juga menguji kemampuan kita dalam memanipulasi angka dan menemukan pola tersembunyi.
Prosesnya, pada dasarnya, adalah tentang mencari ‘kecepatan’ dalam dunia matematika. Semakin terampil kita, semakin cepat pula kita menemukan jawaban soal akar pangkat 3.
Oleh karena itu, akar pangkat tiga dari 100 berada di antara 4 dan 5. Melalui proses perkiraan berulang, kita dapat semakin mempersempit kisarannya.
Menggunakan Kalkulator
Kalkulator menjadi alat yang sangat berguna untuk menghitung akar pangkat tiga. Dengan fungsi kalkulator yang spesifik untuk akar pangkat tiga, kita dapat mendapatkan hasil perhitungan secara langsung dan akurat, terutama untuk bilangan yang kompleks atau besar. Dengan cara ini, kita menghindari perhitungan manual yang panjang dan berpotensi menimbulkan kesalahan.
Langkah-langkah penggunaan kalkulator bervariasi tergantung pada jenis kalkulatornya. Namun, umumnya kita perlu memasukkan bilangan yang akan dihitung akar pangkat tiganya, kemudian menekan tombol fungsi akar pangkat tiga.
Contoh Perhitungan Akar Pangkat 3
Sebagai contoh, mari kita hitung akar pangkat tiga dari 125 menggunakan metode pemfaktoran. 125 dapat difaktorkan menjadi 5 x 5 x 5. Maka, akar pangkat tiga dari 125 adalah 5.
Berikut contoh perhitungan menggunakan kalkulator untuk menghitung akar pangkat tiga dari 216:
- Masukan angka 216 ke kalkulator.
- Tekan tombol fungsi akar pangkat tiga (biasanya √3).
- Hasil yang ditampilkan adalah 6.
Ilustrasi Proses Perhitungan
Proses perhitungan akar pangkat tiga, baik dengan pemfaktoran atau perkiraan, melibatkan langkah-langkah sistematis untuk menemukan bilangan yang jika dipangkatkan tiga sama dengan bilangan yang dicari. Proses ini dapat divisualisasikan dengan diagram pohon pemfaktoran untuk metode pemfaktoran, atau dengan garis bilangan untuk metode perkiraan, untuk memperlihatkan rentang kemungkinan hasil.
Contoh Soal Akar Pangkat 3
Memahami akar pangkat tiga merupakan langkah krusial dalam matematika. Kemampuan ini membuka pintu pemahaman yang lebih dalam terhadap operasi matematika dan aplikasinya dalam berbagai bidang. Berikut ini, kita akan menyelidiki berbagai contoh soal akar pangkat tiga, mulai dari bilangan bulat, pecahan, hingga desimal, untuk memberikan pemahaman yang komprehensif.
Contoh Soal Akar Pangkat 3 dengan Bilangan Bulat
Akar pangkat tiga dari bilangan bulat seringkali melibatkan pengenalan pola dan hubungan antara bilangan. Kita perlu mengenali bilangan yang ketika dikalikan tiga kali menghasilkan bilangan tersebut.
| Soal | Penyelesaian | Jawaban |
|---|---|---|
| √38 | Cari bilangan yang jika dikalikan dengan dirinya sendiri sebanyak 3 kali menghasilkan 8. 2 x 2 x 2 = 8 | 2 |
| √327 | Cari bilangan yang jika dikalikan dengan dirinya sendiri sebanyak 3 kali menghasilkan 27. 3 x 3 x 3 = 27 | 3 |
| √364 | Cari bilangan yang jika dikalikan dengan dirinya sendiri sebanyak 3 kali menghasilkan 64. 4 x 4 x 4 = 64 | 4 |
Contoh Soal Akar Pangkat 3 dengan Bilangan Pecahan
Akar pangkat tiga dari bilangan pecahan memerlukan pemahaman tentang operasi pecahan dan bagaimana mengaplikasikannya pada konsep akar pangkat tiga. Perhatikan bagaimana pembilang dan penyebut dihitung secara terpisah.
| Soal | Penyelesaian | Jawaban |
|---|---|---|
| √3(1/8) | Akar pangkat tiga dari pembilang adalah 1, dan akar pangkat tiga dari penyebut adalah 2. Jadi, hasilnya adalah 1/2. | 1/2 |
| √3(27/64) | Akar pangkat tiga dari 27 adalah 3, dan akar pangkat tiga dari 64 adalah 4. Maka hasilnya adalah 3/4. | 3/4 |
| √3(125/216) | Akar pangkat tiga dari 125 adalah 5, dan akar pangkat tiga dari 216 adalah 6. Jadi hasilnya adalah 5/6. | 5/6 |
Contoh Soal Akar Pangkat 3 dengan Bilangan Desimal
Contoh soal dengan bilangan desimal menekankan pemahaman tentang cara mengonversi desimal ke bentuk pecahan sebelum menghitung akar pangkat tiga. Penting untuk memahami bagaimana mengubah bilangan desimal menjadi pecahan untuk memudahkan perhitungan.
| Soal | Penyelesaian | Jawaban |
|---|---|---|
| √3(0.008) | Ubah 0.008 menjadi pecahan (8/1000). Kemudian, hitung akar pangkat tiga dari pecahan tersebut. Akar pangkat tiga dari 8 adalah 2, dan akar pangkat tiga dari 1000 adalah 10. Jadi hasilnya adalah 2/10 atau 0.2 | 0.2 |
| √3(0.027) | Ubah 0.027 menjadi pecahan (27/1000). Akar pangkat tiga dari 27 adalah 3, dan akar pangkat tiga dari 1000 adalah 10. Jadi hasilnya adalah 3/10 atau 0.3. | 0.3 |
| √3(0.125) | Ubah 0.125 menjadi pecahan (125/1000). Akar pangkat tiga dari 125 adalah 5, dan akar pangkat tiga dari 1000 adalah 10. Jadi hasilnya adalah 5/10 atau 0.5 | 0.5 |
Sifat-Sifat Akar Pangkat 3
Source: idschool.net
Menyelesaikan soal akar pangkat 3 memang butuh ketelitian, bukan? Tapi, pernahkah kamu berpikir, bagaimana jika proses mencari ide produksi untuk sebuah produk baru juga punya tahapan yang sama? Tahap selanjutnya dari proses pencarian ide produksi adalah menentukan target pasar dan menganalisis kebutuhan mereka. Seolah-olah, kita perlu menemukan “akar pangkat 3” dari kebutuhan konsumen untuk menghasilkan produk yang tepat sasaran.
Proses ini juga membutuhkan pemahaman mendalam, sama seperti kita perlu memahami konsep akar pangkat 3 untuk mendapatkan jawaban yang akurat.
Setelah memahami dasar-dasar perhitungan akar pangkat 3, kita akan menyelami sifat-sifatnya yang unik. Sifat-sifat ini tak hanya penting untuk pemahaman konsep, tetapi juga sangat berpengaruh dalam menyelesaikan berbagai persoalan matematika yang melibatkan akar pangkat 3.
Pengaruh Operasi Aritmatika terhadap Akar Pangkat 3
Operasi aritmatika seperti penjumlahan, pengurangan, perkalian, dan pembagian terhadap bilangan yang memiliki akar pangkat 3 akan memengaruhi nilai akar pangkat 3 itu sendiri. Perubahan ini tidak selalu linier dan terkadang rumit untuk diprediksi tanpa pemahaman mendalam tentang sifat-sifatnya.
Sifat-Sifat Akar Pangkat 3
Beberapa sifat penting yang perlu dipahami meliputi sifat distributif, sifat komutatif, dan sifat asosiatif, serta bagaimana sifat-sifat ini berinteraksi dalam perhitungan. Pemahaman terhadap sifat-sifat ini akan membantu dalam menyederhanakan dan mempercepat proses perhitungan.
- Sifat Distributif: Akar pangkat 3 dari suatu perkalian tidak selalu sama dengan perkalian dari akar pangkat 3 masing-masing faktor. Sifat distributif pada akar pangkat 3 tidak berlaku secara umum, sehingga kita harus berhati-hati dalam penerapannya.
- Sifat Komutatif: Sifat komutatif (pertukaran) tidak berlaku pada operasi akar pangkat 3. Urutan bilangan dalam operasi ini berpengaruh terhadap hasilnya.
- Sifat Asosiatif: Sifat asosiatif (pengelompokan) juga tidak berlaku pada operasi akar pangkat 3. Pengelompokan bilangan dalam operasi ini akan memengaruhi hasil akhir.
- Sifat dengan Operasi Lain: Perhatikan bagaimana sifat akar pangkat 3 berinteraksi dengan operasi matematika lainnya. Misalnya, penjumlahan atau pengurangan akar pangkat 3 sering kali tidak bisa disederhanakan secara langsung. Hasilnya biasanya dalam bentuk akar pangkat 3.
Pengaruh Sifat-Sifat terhadap Perhitungan
Pemahaman tentang sifat-sifat ini sangat krusial dalam menyelesaikan soal-soal yang melibatkan akar pangkat 3. Sifat-sifat ini akan membantu kita dalam menyederhanakan perhitungan, menghindari kesalahan, dan menemukan solusi yang tepat.
Contoh: Jika kita ingin menghitung √27 + √8, kita tidak bisa langsung menjumlahkan akarnya. Kita perlu menyederhanakan akar pangkat 3 terlebih dahulu, lalu menjumlahkannya.
Ringkasan Sifat-Sifat Akar Pangkat 3
Berikut ringkasan sifat-sifat penting akar pangkat 3:
- Sifat distributif tidak berlaku.
- Sifat komutatif tidak berlaku.
- Sifat asosiatif tidak berlaku.
- Operasi dengan operasi lain (penjumlahan, pengurangan, perkalian, pembagian) membutuhkan perlakuan khusus.
Penerapan Akar Pangkat 3 dalam Kehidupan Sehari-hari
Akar pangkat tiga, meskipun terkesan rumit dalam perhitungan, memiliki aplikasi yang tak terduga dalam berbagai aspek kehidupan sehari-hari. Dari perhitungan volume hingga desain arsitektur, konsep ini berperan penting dalam menyelesaikan masalah praktis. Mari kita telusuri bagaimana akar pangkat tiga diterapkan dalam kehidupan nyata.
Perhitungan Volume Benda Berbentuk Kubus
Salah satu penerapan paling langsung adalah dalam menghitung volume benda berbentuk kubus. Jika diketahui volume suatu kubus, akar pangkat tiga dari volume tersebut akan memberikan panjang sisi kubus. Misalnya, sebuah kotak kardus berbentuk kubus dengan volume 27 cm 3. Dengan menghitung akar pangkat tiga dari 27, kita memperoleh panjang sisi kubus tersebut adalah 3 cm.
Desain dan Konstruksi Bangunan
Dalam perencanaan dan konstruksi bangunan, perhitungan volume dan dimensi sangat penting. Akar pangkat tiga berperan dalam menentukan dimensi material konstruksi yang dibutuhkan, seperti dalam perhitungan volume beton untuk fondasi atau volume kayu untuk pembuatan balok. Misalnya, untuk membangun kolam renang berbentuk kubus dengan volume tertentu, perlu dihitung panjang sisi kolam untuk menentukan ukuran material yang dibutuhkan.
Penerapan dalam Geometri dan Fisika
Konsep akar pangkat tiga juga muncul dalam berbagai rumus geometri dan fisika. Misalnya, dalam menghitung jari-jari bola jika diketahui volumenya. Rumus ini menghubungkan volume bola dengan jari-jari bola melalui perhitungan akar pangkat tiga. Dalam fisika, akar pangkat tiga dapat ditemukan dalam perhitungan terkait gelombang atau medan listrik, meskipun tidak selalu menjadi fokus utama.
Contoh Kasus: Menentukan Panjang Sisi Kubus
Sebuah perusahaan ingin membuat kotak penyimpanan berbentuk kubus dengan volume 125 liter. Berapa panjang sisi kotak tersebut? Untuk menyelesaikannya, kita perlu menghitung akar pangkat tiga dari 125 liter (atau 125.000 cm 3). Hasilnya adalah 50 cm. Jadi, panjang sisi kotak penyimpanan tersebut adalah 50 cm.
Contoh Kasus: Menentukan Panjang Sisi Akuarium
Seseorang ingin membuat akuarium berbentuk kubus dengan volume 1000 liter. Berapakah panjang sisi akuarium tersebut? Dengan menghitung akar pangkat tiga dari 1000 liter (atau 1.000.000 cm 3), kita mendapatkan panjang sisi akuarium adalah 100 cm.
Perbedaan Akar Pangkat 3 dengan Operasi Matematika Lainnya
Akar pangkat tiga, berbeda dengan operasi matematika dasar seperti penjumlahan, pengurangan, perkalian, dan pembagian. Perbedaan mendasar terletak pada sifat operasi dan cara perhitungannya. Akar pangkat tiga mencari angka yang, ketika dikalikan dengan dirinya sendiri tiga kali, menghasilkan angka tertentu. Mari kita telusuri lebih dalam perbedaan-perbedaannya.
Menghitung akar pangkat tiga memang terlihat sederhana, namun sebenarnya melibatkan proses kompleks, bukan? Bayangkan, kita sedang mencari keseimbangan, seperti proses penyambungan komponen pada metode keseimbangan menggunakan proses penyambungan komponen pada metode keseimbangan menggunakan. Setiap elemen harus pas dan tepat posisinya, sama seperti bagaimana kita mencari nilai yang jika dikalikan tiga kali menghasilkan angka tertentu dalam soal akar pangkat tiga.
Proses ini menuntut ketelitian yang tinggi, bukan hanya dalam perhitungan matematika, tetapi juga dalam memahami konteks soal akar pangkat tiga itu sendiri.
Perbandingan dengan Operasi Matematika Lainnya
Berikut tabel yang membandingkan akar pangkat tiga dengan operasi matematika lainnya:
| Operasi | Cara Perhitungan | Hasil | Contoh |
|---|---|---|---|
| Penjumlahan | Menambahkan dua atau lebih angka | Satu angka | 2 + 3 = 5 |
| Pengurangan | Mengurangkan satu angka dari angka lainnya | Satu angka | 5 – 2 = 3 |
| Perkalian | Mengalikan dua atau lebih angka | Satu angka | 2 x 3 = 6 |
| Pembagian | Membagi satu angka dengan angka lainnya | Satu angka (atau pecahan) | 6 / 2 = 3 |
| Akar Pangkat 3 | Mencari angka yang, ketika dikalikan dengan dirinya sendiri tiga kali, menghasilkan angka tertentu | Satu angka | ∛8 = 2 (karena 2 x 2 x 2 = 8) |
Tabel di atas menunjukkan perbedaan mendasar dalam cara perhitungan. Operasi dasar hanya melibatkan manipulasi angka dengan operasi sederhana, sementara akar pangkat tiga melibatkan pencarian angka yang ketika dikalikan berulang kali menghasilkan angka target.
Perbedaan dalam Cara Perhitungan
Perbedaan dalam cara perhitungan ini sangat penting. Penjumlahan, pengurangan, perkalian, dan pembagian memiliki algoritma perhitungan yang relatif sederhana dan langsung. Akar pangkat tiga, terutama untuk angka yang lebih besar atau tidak sempurna pangkat tiga, seringkali memerlukan teknik yang lebih rumit, seperti metode pembagian berulang atau menggunakan tabel/kalkulator.
Perbedaan dalam Konsep Terkait
Akar pangkat tiga berbeda dari konsep lainnya yang terkait, seperti akar pangkat dua. Akar pangkat dua mencari angka yang, ketika dikalikan dengan dirinya sendiri, menghasilkan angka target. Akar pangkat tiga berbeda karena mencari angka yang, ketika dikalikan dengan dirinya sendiri sebanyak tiga kali, menghasilkan angka target. Perbedaan ini terletak pada eksponen yang digunakan dalam perhitungan.
Bilangan yang Memiliki Akar Pangkat 3 Sempurna
Setelah memahami dasar-dasar akar pangkat 3, mari kita telusuri bilangan-bilangan yang memiliki akar pangkat 3 sempurna. Bilangan-bilangan ini, yang disebut bilangan kubik, memiliki sifat unik yang memudahkan perhitungan dan pemahaman dalam berbagai konteks matematika.
Daftar Bilangan Kubik
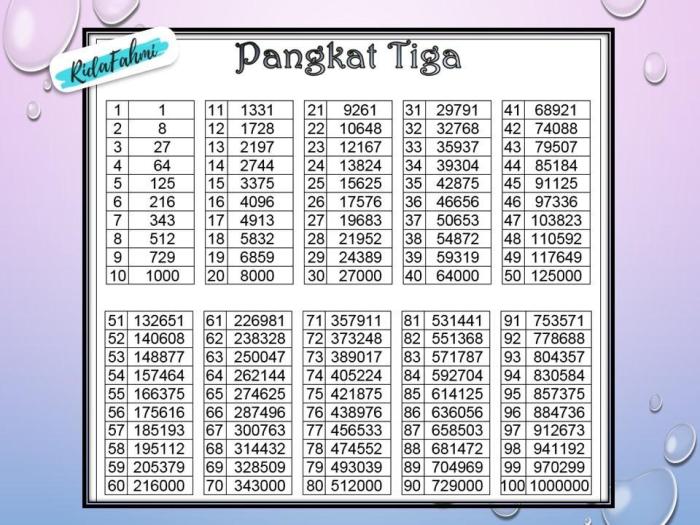
Bilangan kubik adalah hasil perkalian suatu bilangan bulat dengan dirinya sendiri sebanyak tiga kali. Dengan kata lain, jika kita mengalikan suatu bilangan bulat dengan dirinya sendiri dua kali, hasilnya adalah bilangan kuadrat, sedangkan untuk bilangan kubik, perkaliannya dilakukan sebanyak tiga kali. Berikut beberapa contoh bilangan kubik:
- 1 3 = 1
- 2 3 = 8
- 3 3 = 27
- 4 3 = 64
- 5 3 = 125
- 6 3 = 216
- 7 3 = 343
- 8 3 = 512
- 9 3 = 729
- 10 3 = 1000
Tabel Bilangan dan Akar Pangkat 3
Untuk mempermudah visualisasi, berikut tabel yang merangkum bilangan kubik dan akar pangkat 3-nya:
| Bilangan | Akar Pangkat 3 |
|---|---|
| 1 | 1 |
| 8 | 2 |
| 27 | 3 |
| 64 | 4 |
| 125 | 5 |
| 216 | 6 |
| 343 | 7 |
| 512 | 8 |
| 729 | 9 |
| 1000 | 10 |
Menentukan Bilangan Kubik
Cara menentukan apakah suatu bilangan merupakan bilangan kubik adalah dengan mencari akar pangkat 3 dari bilangan tersebut. Jika hasilnya merupakan bilangan bulat, maka bilangan tersebut adalah bilangan kubik. Contohnya, akar pangkat 3 dari 27 adalah 3, yang merupakan bilangan bulat, sehingga 27 adalah bilangan kubik. Sebaliknya, akar pangkat 3 dari 20 tidak menghasilkan bilangan bulat, sehingga 20 bukan bilangan kubik.
Secara umum, cara menentukan apakah suatu bilangan merupakan bilangan kubik adalah dengan menghitung akar pangkat 3 dari bilangan tersebut. Jika hasilnya adalah bilangan bulat, maka bilangan tersebut merupakan bilangan kubik.
Akar Pangkat 3 dan Bilangan Negatif
Dalam dunia matematika, kita seringkali berhadapan dengan akar pangkat tiga. Namun, bagaimana jika bilangan yang kita akar pangkatkan adalah bilangan negatif? Apakah aturannya sama dengan bilangan positif? Mari kita telusuri lebih dalam.
Menghitung Akar Pangkat 3 dari Bilangan Negatif
Perbedaan utama antara akar pangkat tiga dari bilangan positif dan negatif terletak pada tanda hasilnya. Untuk bilangan positif, akar pangkat tiga selalu positif. Namun, untuk bilangan negatif, akar pangkat tiga juga akan bernilai negatif.
Aturan Tanda pada Akar Pangkat 3
Aturan ini berlaku secara konsisten. Jika kita mencari akar pangkat tiga dari bilangan negatif, hasilnya akan selalu negatif. Hal ini dapat dipahami dengan melihat definisi dari akar pangkat tiga. Akar pangkat tiga dari suatu bilangan a, dilambangkan sebagai 3√ a, adalah bilangan x yang jika dipangkatkan tiga hasilnya sama dengan a, yaitu x3 = a.
Dalam konteks bilangan negatif, ini akan menghasilkan nilai x yang juga negatif.
Contoh Soal dan Penyelesaian
Mari kita lihat beberapa contoh konkret:
- Contoh 1: 3√(-8) = ?
Untuk mencari akar pangkat tiga dari -8, kita perlu mencari bilangan yang jika dipangkatkan tiga hasilnya sama dengan -8. Jawabannya adalah -2, karena (-2) 3 = -8. Jadi, 3√(-8) = -2.
Menarik, bukan? Soal akar pangkat 3, meski tampak sederhana, justru terhubung dengan konsep-konsep biologi yang lebih kompleks. Bayangkan, jika kita mau meneliti lebih dalam, kita akan menemukan bahwa berikut adalah komponen kimiawi organik penyusun sel adalah seperti karbohidrat, lipid, protein, dan asam nukleat. berikut adalah komponen kimiawi organik penyusun sel adalah Semua itu, pada akhirnya, memiliki peran dalam membangun struktur dan fungsi sel, yang juga berimplikasi pada bagaimana kita memahami penyelesaian soal akar pangkat 3 dalam konteks yang lebih luas.
Ini menunjukkan betapa eratnya hubungan matematika dan biologi. Maka, soal akar pangkat 3 tidak hanya soal hitung-hitungan, tapi juga tentang pemahaman dasar akan elemen-elemen kehidupan.
- Contoh 2: 3√(-27) = ?
Bilangan yang jika dipangkatkan tiga hasilnya -27 adalah -3. Dengan demikian, 3√(-27) = -3.
- Contoh 3: 3√(-64) = ?
Bilangan yang jika dipangkatkan tiga hasilnya -64 adalah -4. Maka, 3√(-64) = -4.
Perbedaan dengan Akar Pangkat 3 dari Bilangan Positif
Perbedaan mendasarnya terletak pada tanda hasil. Jika kita menghitung akar pangkat tiga dari bilangan positif, hasilnya akan selalu positif. Sebaliknya, jika kita menghitung akar pangkat tiga dari bilangan negatif, hasilnya akan selalu negatif. Ini merupakan konsekuensi langsung dari definisi akar pangkat tiga itu sendiri.
Strategi Pembelajaran Akar Pangkat 3
Mempelajari akar pangkat 3 mungkin terasa menantang, tetapi dengan strategi yang tepat, konsep ini bisa dipahami dengan lebih mudah. Pemahaman yang mendalam tentang konsep ini akan membuka pintu untuk mengaplikasikannya dalam berbagai bidang, mulai dari matematika hingga fisika dan teknik.
Menggunakan Pola dan Pola Bilangan
Memahami pola bilangan kubik (hasil perkalian suatu bilangan dengan dirinya sendiri sebanyak tiga kali) merupakan kunci untuk menguasai akar pangkat 3. Mempelajari pola-pola ini akan membantu dalam memprediksi akar pangkat 3 dari bilangan-bilangan kecil hingga menengah. Contohnya, jika kita mengetahui bahwa 2 3 = 8, maka √ 38 = 2. Penggunaan tabel bilangan kubik dan pola-pola yang muncul dapat mempercepat proses pemahaman.
Memvisualisasikan Kubus
Menghubungkan konsep akar pangkat 3 dengan visualisasi kubus sangat membantu. Bayangkan bagaimana bilangan-bilangan kubik merepresentasikan volume kubus dengan sisi tertentu. Misalnya, jika volume kubus adalah 27 satuan kubik, maka panjang sisinya adalah akar pangkat 3 dari 27, yaitu 3. Visualisasi ini dapat membantu dalam memahami hubungan antara bilangan dan bentuk geometri.
Latihan dan Pengulangan
Latihan rutin adalah kunci untuk menguasai materi akar pangkat 3. Mulailah dengan soal-soal sederhana dan secara bertahap tingkatkan kesulitannya. Lakukan latihan berulang-ulang untuk memperkuat pemahaman dan meningkatkan kecepatan dalam menghitung. Solusi dan penjelasan yang detail untuk setiap soal sangatlah penting untuk mengidentifikasi dan memperbaiki kesalahan.
Menggunakan Alat Bantu
Terdapat beberapa alat bantu yang dapat mempermudah proses pembelajaran akar pangkat 3, seperti aplikasi kalkulator atau tabel akar pangkat 3. Penggunaan alat bantu ini dapat mempercepat proses perhitungan dan mengurangi kesalahan, namun pemahaman konsep tetap menjadi prioritas utama.
Menghafal Akar Pangkat 3 Bilangan Kecil
Menghafal akar pangkat 3 dari bilangan-bilangan kecil (misalnya 1, 2, 3, 4, 5, dan seterusnya) dapat mempercepat proses perhitungan. Tabel atau kartu flashcard dapat menjadi alat bantu yang efektif untuk menghafal bilangan-bilangan tersebut. Pengulangan dan latihan berkelanjutan akan memperkuat kemampuan menghafal.
Menerapkan Konsep dalam Soal-Soal
Menerapkan konsep akar pangkat 3 dalam berbagai macam soal adalah langkah penting untuk memahami penerapannya dalam kehidupan sehari-hari. Semakin banyak soal yang dikerjakan, semakin terbiasa dan mahir dalam menyelesaikan soal-soal yang berkaitan dengan akar pangkat 3. Perhatikan langkah-langkah penyelesaian yang benar dan analisa kesalahan.
Latihan Soal Akar Pangkat 3
Source: z-dn.net
Menguasai akar pangkat tiga membutuhkan latihan yang berkelanjutan. Latihan soal berikut dirancang untuk membantu Anda mengasah pemahaman dan keterampilan dalam menyelesaikan soal-soal akar pangkat tiga dengan berbagai tingkat kesulitan.
Soal Latihan Akar Pangkat 3
Berikut ini lima soal latihan akar pangkat tiga dengan tingkat kesulitan yang berbeda, dilengkapi dengan kunci jawaban dan langkah-langkah penyelesaiannya. Mempelajari langkah-langkah penyelesaian sangat penting untuk memahami konsep dan menghindari kesalahan umum.
| No | Soal | Jawaban | Cara Penyelesaian |
|---|---|---|---|
| 1 | Berapakah akar pangkat tiga dari 27? | 3 |
Untuk mencari akar pangkat tiga dari 27, kita perlu mencari bilangan yang jika dikalikan tiga kali dengan dirinya sendiri menghasilkan 27. 3 x 3 x 3 = 27, sehingga akar pangkat tiga dari 27 adalah 3. |
| 2 | Hitunglah nilai dari ∛125. | 5 |
∛125 sama dengan mencari bilangan yang dikalikan tiga kali menghasilkan 125. 5 x 5 x 5 = 125, sehingga jawabannya adalah 5. |
| 3 | Tentukan nilai dari ∛-64. | -4 |
Akar pangkat tiga dari bilangan negatif juga menghasilkan bilangan negatif. -4 x -4 x -4 = -64. Jadi, akar pangkat tiga dari -64 adalah -4. |
| 4 | Berapakah akar pangkat tiga dari 343? | 7 |
Kita perlu mencari bilangan yang jika dikalikan tiga kali dengan dirinya sendiri menghasilkan 343. 7 x 7 x 7 = 343, sehingga jawabannya adalah 7. |
| 5 | Hitunglah ∛100000 | 100 |
Dalam kasus ini, kita mencari bilangan yang dikalikan tiga kali menghasilkan 100000. 100 x 100 x 100 = 100000. Jadi, akar pangkat tiga dari 100000 adalah 100. |
Ulasan Penutup
Dalam mempelajari akar pangkat 3, kita telah melihat betapa pentingnya pemahaman konsep dasar dan aplikasi dalam kehidupan sehari-hari. Dengan strategi yang tepat dan latihan soal yang cukup, Anda dapat menguasai topik ini dengan percaya diri. Semoga penjelasan ini memberikan gambaran yang komprehensif dan memudahkan pemahaman Anda tentang akar pangkat 3.
FAQ Umum
Bagaimana cara menentukan apakah suatu bilangan memiliki akar pangkat 3 sempurna?
Untuk menentukan apakah suatu bilangan memiliki akar pangkat 3 sempurna, kita perlu memeriksa apakah bilangan tersebut dapat difaktorkan menjadi hasil perkalian tiga bilangan yang sama.
Apa perbedaan antara akar pangkat 3 dan akar pangkat 2?
Perbedaan mendasar terletak pada jumlah faktor yang dibutuhkan. Akar pangkat 2 memerlukan dua faktor yang sama, sedangkan akar pangkat 3 memerlukan tiga faktor yang sama.
Bagaimana cara menghitung akar pangkat 3 dari bilangan negatif?
Akar pangkat 3 dari bilangan negatif adalah bilangan negatif. Misalnya, akar pangkat 3 dari -8 adalah -2.