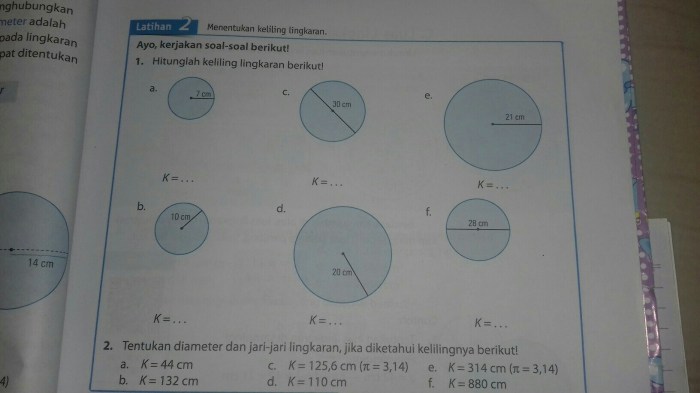
Soal lingkaran kelas 6, sebuah materi yang menarik untuk dipelajari. Lingkaran, sebagai bentuk geometri yang unik, memiliki berbagai aplikasi dalam kehidupan sehari-hari, mulai dari roda sepeda hingga desain arsitektur. Mari kita telusuri lebih dalam tentang rumus, jenis-jenis soal, dan strategi pemecahan masalah yang efektif untuk menguasai materi ini.
Dalam pembahasan soal lingkaran kelas 6 ini, kita akan memulai dengan definisi dan unsur-unsur lingkaran. Selanjutnya, kita akan mempelajari rumus-rumus penting untuk menghitung keliling dan luas lingkaran. Kita juga akan mengidentifikasi berbagai jenis soal yang mungkin muncul, termasuk soal cerita, dan langkah-langkah penyelesaiannya. Terakhir, kita akan membahas strategi pemecahan masalah, tips belajar, dan contoh-contoh soal latihan untuk mengasah pemahaman.
Definisi Lingkaran
Lingkaran merupakan salah satu bangun datar yang paling fundamental dalam geometri. Bentuknya yang simetris dan karakteristiknya yang unik membuatnya menjadi objek kajian yang menarik. Memahami definisi dan unsur-unsurnya akan membuka wawasan kita terhadap kegunaan lingkaran dalam kehidupan sehari-hari.
Definisi Matematis Lingkaran
Secara matematis, lingkaran didefinisikan sebagai himpunan semua titik pada bidang datar yang berjarak sama terhadap suatu titik tetap. Titik tetap tersebut disebut pusat lingkaran, dan jarak yang sama tersebut disebut jari-jari.
Unsur-unsur Lingkaran
Lingkaran memiliki beberapa unsur penting yang perlu dipahami. Berikut penjelasan singkatnya:
- Jari-jari (r): Segmen garis yang menghubungkan pusat lingkaran dengan sembarang titik pada lingkaran.
- Diameter (d): Segmen garis yang menghubungkan dua titik pada lingkaran dan melewati pusat lingkaran. Panjang diameter sama dengan dua kali panjang jari-jari (d = 2r).
- Titik Pusat: Titik di tengah lingkaran yang sama jaraknya terhadap semua titik pada lingkaran.
- Busur: Bagian dari lingkaran yang dibatasi oleh dua titik pada lingkaran.
- Tali Busur: Segmen garis yang menghubungkan dua titik pada lingkaran.
- Apotema: Garis tegak lurus dari titik pusat ke tali busur, membagi tali busur menjadi dua bagian sama panjang.
- Juring: Daerah yang dibatasi oleh dua jari-jari dan busur yang menghubungkan kedua jari-jari tersebut.
- Tembereng: Daerah yang dibatasi oleh tali busur dan busur yang diikat oleh tali busur tersebut.
Perbandingan Lingkaran dengan Bentuk Geometri Lainnya
Berikut tabel perbandingan lingkaran dengan beberapa bentuk geometri lainnya:
| Bentuk | Karakteristik |
|---|---|
| Lingkaran | Himpunan titik yang berjarak sama terhadap satu titik pusat. |
| Segitiga | Memiliki tiga sisi dan tiga sudut. |
| Persegi Panjang | Memiliki empat sisi dengan sudut siku-siku. |
| Jajar Genjang | Memiliki dua pasang sisi sejajar. |
Ilustrasi Sketsa Lingkaran
Bayangkan sebuah lingkaran dengan titik pusat O. Dari titik pusat O, terdapat beberapa jari-jari yang menghubungkan ke titik-titik pada lingkaran. Garis yang menghubungkan dua titik pada lingkaran dan melewati titik pusat disebut diameter. Ada pula tali busur yang menghubungkan dua titik pada lingkaran. Perhatikan bagaimana semua jarak dari titik pusat ke titik pada lingkaran selalu sama, inilah ciri khas lingkaran.
Contoh Penerapan Konsep Lingkaran
Konsep lingkaran diterapkan dalam berbagai aspek kehidupan sehari-hari, mulai dari yang sederhana hingga yang kompleks. Beberapa contohnya antara lain:
- Roda mobil: Bentuk roda mobil yang melingkar memungkinkan mobilitas yang mudah dan efisien.
- Jam dinding: Jarum jam yang bergerak melingkar menunjukkan waktu.
- Planet mengelilingi matahari: Gerakan planet mengelilingi matahari mengikuti lintasan melingkar (atau lebih tepatnya elips).
- Taman dan kolam renang: Bentuk melingkar pada taman atau kolam renang sering digunakan untuk keindahan dan simetri.
- Struktur bangunan: Banyak struktur bangunan menggunakan konsep lingkaran dalam desainnya untuk kekuatan dan estetika.
Rumus-rumus Lingkaran
Lingkaran, sebagai salah satu bentuk geometri yang paling mendasar, memiliki karakteristik unik yang membuatnya menarik untuk dipelajari. Pemahaman tentang rumus-rumusnya sangat penting untuk menghitung berbagai besaran pada lingkaran, mulai dari keliling hingga luas.
Rumus Keliling Lingkaran
Keliling lingkaran adalah panjang garis yang mengelilingi lingkaran tersebut. Rumus yang digunakan untuk menghitung keliling lingkaran melibatkan jari-jari (r) atau diameter (d) lingkaran. Hubungan ini mencerminkan bagaimana ukuran jari-jari atau diameter memengaruhi panjang keliling.
Soal lingkaran di kelas 6, seringkali melibatkan konsep-konsep dasar geometri, bukan? Nah, menariknya, proses penentuan puasa awal Ramadan juga melibatkan perhitungan astronomi yang rumit. Penentuan puasa awal Ramadan ditentukan melalui pengamatan hilal, yang pada akhirnya berpengaruh pada perhitungan posisi bulan dan waktu. Proses ini, meskipun tampak berbeda, sebenarnya punya kaitan dengan ketelitian dalam menentukan suatu titik, sudut, atau lingkaran.
Bukankah soal-soal lingkaran di kelas 6 juga menguji kemampuan kita dalam memahami konsep-konsep seperti jari-jari, diameter, dan keliling? Jadi, kita bisa melihat bagaimana konsep-konsep dasar dalam matematika, bahkan geometri sederhana, terhubung dengan aspek kehidupan sehari-hari.
Keliling (K) = 2 × π × r atau K = π × d
Dimana:
- K = Keliling lingkaran
- π (pi) = Konstanta matematika yang kira-kira bernilai 3,14
- r = Jari-jari lingkaran
- d = Diameter lingkaran (diameter adalah dua kali jari-jari)
Rumus Luas Lingkaran
Luas lingkaran adalah ukuran daerah yang dibatasi oleh lingkaran tersebut. Rumus luas lingkaran juga melibatkan jari-jari (r) dan konstanta π.
Luas (L) = π × r2
Dimana:
- L = Luas lingkaran
- π (pi) = Konstanta matematika yang kira-kira bernilai 3,14
- r = Jari-jari lingkaran
Tabel Rumus-rumus Lingkaran
| Besaran | Rumus | Variabel |
|---|---|---|
| Keliling | K = 2 × π × r atau K = π × d | K (Keliling), π (pi), r (Jari-jari), d (Diameter) |
| Luas | L = π × r2 | L (Luas), π (pi), r (Jari-jari) |
Contoh Perhitungan
Misalkan terdapat lingkaran dengan jari-jari 7 cm. Kita ingin menghitung keliling dan luas lingkaran tersebut.
Menghitung Keliling:
K = 2 × π × r = 2 × 3,14 × 7 cm = 43,96 cm
Menghitung Luas:
L = π × r 2 = 3,14 × 7 2 cm 2 = 153,86 cm 2
Perbedaan dan Keterkaitan Keliling dan Luas
Keliling dan luas lingkaran berbeda dalam hal yang diukur. Keliling mengukur panjang garis yang mengelilingi lingkaran, sedangkan luas mengukur daerah yang dibatasi oleh lingkaran. Meskipun berbeda, keduanya saling terkait melalui jari-jari lingkaran. Jari-jari berperan sebagai kunci penghubung dalam perhitungan kedua besaran tersebut.
Jenis-jenis Soal Lingkaran Kelas 6
Source: z-dn.net
Materi lingkaran di kelas 6 tak hanya seputar definisi dan rumus, tetapi juga beragam soal yang menguji pemahaman siswa. Menguasai berbagai jenis soal ini penting untuk meraih hasil maksimal. Mari kita telusuri jenis-jenis soal yang sering muncul dan bagaimana mengatasinya!
Perhitungan Keliling dan Luas Lingkaran
Soal-soal ini mengharuskan siswa memahami rumus keliling dan luas lingkaran. Perhitungannya beragam, mulai dari mencari keliling jika diketahui jari-jari atau diameter, atau mencari luas jika diketahui salah satu unsur tersebut. Contohnya, jika diketahui jari-jari lingkaran 7 cm, berapakah keliling dan luasnya? Menghitung keliling dan luas melibatkan penggunaan rumus yang tepat. Ketelitian dalam mengaplikasikan rumus dan melakukan perhitungan menjadi kunci kesuksesan.
- Soal mencari keliling lingkaran dengan diameter atau jari-jari yang diketahui.
- Soal mencari luas lingkaran dengan diameter atau jari-jari yang diketahui.
- Soal cerita yang melibatkan perhitungan keliling atau luas lingkaran, misalnya menghitung panjang kawat untuk membuat kerangka lingkaran atau luas alas sebuah kolam berbentuk lingkaran.
Soal Cerita Terkait Lingkaran
Soal cerita menantang siswa untuk mengaplikasikan pemahaman konsep lingkaran dalam situasi nyata. Siswa perlu mengidentifikasi informasi yang relevan, memilih rumus yang tepat, dan menyelesaikan perhitungan. Contoh soal cerita bisa berupa menghitung panjang tali yang dibutuhkan untuk mengikat sebuah taman berbentuk lingkaran, atau menghitung luas taman bermain berbentuk setengah lingkaran.
Contoh soal: Sebuah taman berbentuk lingkaran memiliki diameter 14 meter. Berapa meter panjang pagar yang dibutuhkan untuk mengelilingi taman tersebut?
Unsur-unsur Lingkaran
Soal ini fokus pada pemahaman siswa tentang unsur-unsur lingkaran, seperti jari-jari, diameter, dan titik pusat. Soal-soal ini bisa berupa pertanyaan langsung atau soal cerita yang mengharuskan siswa mengidentifikasi unsur-unsur lingkaran dalam gambar atau situasi tertentu. Contoh soal: Pada gambar lingkaran di bawah ini, tunjukkan jari-jari dan diameternya.
Tabel Perbedaan Tipe Soal
| Tipe Soal | Deskripsi | Contoh |
|---|---|---|
| Perhitungan Keliling dan Luas | Menghitung keliling atau luas lingkaran dengan data jari-jari atau diameter. | Jika jari-jari lingkaran 5 cm, hitung keliling dan luasnya. |
| Soal Cerita | Menggunakan konsep lingkaran dalam situasi nyata. | Sebuah taman berbentuk lingkaran berdiameter 20 meter. Berapa meter panjang pagar yang dibutuhkan untuk mengelilingi taman? |
| Unsur-unsur Lingkaran | Mengidentifikasi jari-jari, diameter, dan titik pusat lingkaran. | Pada gambar di bawah ini, manakah yang merupakan jari-jari dan diameter lingkaran? |
Contoh Soal dan Penyelesaian
Memahami konsep keliling dan luas lingkaran tak lengkap tanpa latihan soal. Mari kita telusuri bagaimana menghitungnya dengan berbagai kasus, mulai dari soal sederhana hingga soal cerita yang lebih menantang.
Menghitung Keliling Lingkaran
Untuk menghitung keliling lingkaran, kita perlu mengetahui jari-jarinya. Rumus keliling lingkaran adalah 2πr, di mana r adalah jari-jari dan π (pi) kira-kira 3,14.
Contoh Soal: Sebuah lingkaran memiliki jari-jari 7 cm. Berapakah kelilingnya?
- Identifikasi Data: Jari-jari (r) = 7 cm, π ≈ 3,14
- Penerapan Rumus: Keliling = 2πr = 2 × 3,14 × 7 cm
- Perhitungan: Keliling = 43,96 cm
- Kesimpulan: Keliling lingkaran tersebut adalah 43,96 cm.
Menghitung Luas Lingkaran
Untuk menghitung luas lingkaran, kita perlu mengetahui jari-jarinya atau diameternya. Rumus luas lingkaran adalah πr 2, di mana r adalah jari-jari dan π (pi) kira-kira 3,14.
Contoh Soal: Sebuah lingkaran memiliki diameter 14 cm. Berapakah luasnya?
- Identifikasi Data: Diameter = 14 cm, maka jari-jari (r) = 14 cm / 2 = 7 cm, π ≈ 3,14
- Penerapan Rumus: Luas = πr 2 = 3,14 × 7 2 cm 2
- Perhitungan: Luas = 3,14 × 49 cm 2 = 153,86 cm 2
- Kesimpulan: Luas lingkaran tersebut adalah 153,86 cm 2.
Contoh Soal Cerita
Berikut contoh soal cerita yang menggabungkan perhitungan keliling dan luas lingkaran.
Contoh Soal: Seorang tukang kebun ingin membuat taman berbentuk lingkaran dengan diameter 10 meter. Dia ingin memasang pagar di sekeliling taman. Berapa meter pagar yang dibutuhkan? Jika dia ingin memasang penutup rumput di taman, berapa luas taman yang perlu ditutup rumput?
- Menentukan Keliling: Diameter = 10 meter, maka jari-jari (r) = 5 meter. Keliling = 2πr = 2 × 3,14 × 5 meter = 31,4 meter
- Menentukan Luas: Luas = πr 2 = 3,14 × 5 2 meter 2 = 78,5 meter 2
- Kesimpulan: Tukang kebun membutuhkan 31,4 meter pagar dan luas taman yang perlu ditutup rumput adalah 78,5 meter 2.
Strategi Pemecahan Masalah Soal Lingkaran
Memahami lingkaran bukan hanya menghafal rumus, tetapi juga mengembangkan kemampuan memecahkan masalah. Berikut beberapa strategi penting untuk menghadapi soal-soal lingkaran dengan lebih percaya diri.
Langkah-langkah Memecahkan Soal Lingkaran
Kemampuan memecahkan masalah soal lingkaran dibangun melalui tahapan yang sistematis. Berikut langkah-langkah yang dapat diikuti:
- Memahami Pertanyaan: Bacalah soal dengan cermat. Identifikasi apa yang ditanyakan dan apa yang diketahui. Tandai informasi penting seperti jari-jari, diameter, keliling, atau luas.
- Menggambar Sketsa: Menggambar sketsa lingkaran dapat membantu memvisualisasikan masalah. Tandai informasi yang diketahui pada sketsa tersebut. Hal ini akan membantu mengidentifikasi hubungan antara bagian-bagian lingkaran.
- Mengidentifikasi Rumus yang Relevan: Setelah memahami pertanyaan dan menggambar sketsa, tentukan rumus matematika yang sesuai dengan permasalahan yang dihadapi. Apakah yang dicari adalah keliling, luas, jari-jari, atau diameter? Pilih rumus yang tepat.
- Substitusi Nilai: Masukkan nilai-nilai yang diketahui ke dalam rumus yang dipilih. Pastikan satuan ukuran konsisten (misalnya, semua dalam sentimeter atau meter).
- Menghitung dan Menuliskan Jawaban: Lakukan perhitungan dengan teliti. Tuliskan jawaban dengan satuan yang benar. Jangan lupa untuk mengecek kembali perhitungan dan satuan.
Tips dan Trik dalam Menyelesaikan Soal Lingkaran
Berikut beberapa tips dan trik yang dapat membantu dalam menyelesaikan soal lingkaran:
- Perhatikan Satuan: Pastikan satuan ukuran yang digunakan konsisten dalam perhitungan.
- Gambar Sketsa: Gambar sketsa lingkaran untuk memvisualisasikan masalah dan memudahkan pemahaman.
- Ingat Definisi: Ketahui definisi penting, seperti jari-jari, diameter, dan keliling lingkaran. Ini akan membantu memahami hubungan antar bagian lingkaran.
- Pahami Konteks Soal: Jangan hanya terpaku pada rumus. Pahami konteks soal untuk menentukan rumus yang tepat.
- Latih Berulang: Latihan soal secara berulang akan meningkatkan pemahaman dan kemampuan memecahkan masalah.
Mengidentifikasi Informasi Penting dalam Soal
Kemampuan mengidentifikasi informasi penting sangat krusial dalam memecahkan soal lingkaran. Perhatikan poin-poin berikut:
- Kata Kunci: Cari kata kunci yang mengindikasikan besaran yang dicari (misalnya, “keliling,” “luas,” “jari-jari”).
- Nilai Numerik: Catat nilai-nilai numerik yang diberikan dalam soal, serta satuannya.
- Hubungan Antar Bagian: Pahami hubungan antara jari-jari, diameter, keliling, dan luas lingkaran.
Contoh Penerapan Strategi, Soal lingkaran kelas 6
Misalnya, soal: “Sebuah taman berbentuk lingkaran memiliki diameter 14 meter. Berapa keliling taman tersebut?”
- Memahami Pertanyaan: Ditanyakan keliling taman. Diketahui diameter = 14 meter.
- Menggambar Sketsa: Gambar sketsa lingkaran dan tandai diameternya.
- Mengidentifikasi Rumus: Rumus keliling lingkaran = π × diameter.
- Substitusi Nilai: Keliling = π × 14 meter.
- Menghitung dan Menuliskan Jawaban: Misalnya, π = 22/7. Maka, Keliling = (22/7) × 14 = 44 meter.
Flowchart Menyelesaikan Soal Lingkaran
| Langkah | Deskripsi |
|---|---|
| 1. Memahami Soal | Bacalah soal dengan cermat. Identifikasi apa yang ditanyakan dan apa yang diketahui. |
| 2. Gambar Sketsa | Gambar sketsa lingkaran dan tandai informasi yang diketahui. |
| 3. Pilih Rumus | Pilih rumus yang tepat berdasarkan apa yang ditanyakan (keliling, luas, jari-jari, diameter). |
| 4. Substitusi Nilai | Masukkan nilai-nilai yang diketahui ke dalam rumus. |
| 5. Hitung dan Jawab | Lakukan perhitungan dan tuliskan jawaban dengan satuan yang benar. |
Konsep Kunci Lingkaran
Memahami lingkaran bukan sekadar menghafal rumus, tetapi memahami hubungan antar unsur-unsurnya. Konsep-konsep kunci ini akan membantu kita memahami lebih dalam bagaimana lingkaran bekerja dan diterapkan dalam berbagai masalah.
Unsur-Unsur Lingkaran
Lingkaran tersusun dari berbagai unsur yang saling terkait. Memahami hubungan antar unsur-unsur ini sangat penting untuk menyelesaikan soal-soal yang berkaitan dengan lingkaran.
- Jari-jari (r): Jarak dari pusat lingkaran ke titik pada keliling lingkaran. Jari-jari memiliki peran penting dalam menghitung luas dan keliling lingkaran.
- Diameter (d): Garis lurus yang menghubungkan dua titik pada keliling lingkaran dan melewati pusat lingkaran. Diameter sama dengan dua kali jari-jari (d = 2r).
- Keliling (K): Panjang garis tepi lingkaran. Rumus keliling lingkaran bergantung pada jari-jari atau diameter.
- Luas (L): Luas daerah yang dibatasi oleh lingkaran. Rumus luas lingkaran bergantung pada jari-jari.
- Busur: Bagian dari keliling lingkaran yang dibatasi oleh dua jari-jari. Panjang busur bergantung pada besar sudut pusat yang dibentuk oleh kedua jari-jari tersebut.
- Sudut Pusat: Sudut yang dibentuk oleh dua jari-jari yang berpotongan di pusat lingkaran. Besar sudut pusat berperan penting dalam menentukan panjang busur dan luas juring.
- Juring: Daerah yang dibatasi oleh dua jari-jari dan busur yang menghubungkan kedua ujung jari-jari tersebut. Luas juring bergantung pada besar sudut pusat dan jari-jari.
Hubungan Antar Unsur
Unsur-unsur lingkaran saling terkait dan memengaruhi satu sama lain. Memahami keterkaitan ini sangat penting dalam menyelesaikan soal-soal yang kompleks.
| Unsur | Hubungan dengan Unsur Lain | Contoh Penerapan |
|---|---|---|
| Jari-jari | Merupakan setengah dari diameter. Berpengaruh pada keliling dan luas lingkaran. | Jika jari-jari lingkaran 5 cm, maka diameternya 10 cm. |
| Diameter | Dua kali jari-jari. | Jika diameter lingkaran 20 cm, maka jari-jarinya 10 cm. |
| Keliling | Dipengaruhi oleh jari-jari atau diameter. | Keliling lingkaran dengan jari-jari 7 cm adalah 43,98 cm. |
| Luas | Dipengaruhi oleh jari-jari. | Luas lingkaran dengan jari-jari 10 cm adalah 314 cm2. |
Penerapan dalam Soal-Soal
Konsep-konsep ini dapat diaplikasikan dalam berbagai soal, mulai dari menghitung keliling dan luas, hingga menentukan panjang busur dan luas juring.
- Contoh 1: Tentukan keliling lingkaran dengan jari-jari 7 cm. (Jawaban: Keliling = 2πr = 2π(7) = 43,98 cm)
- Contoh 2: Tentukan luas lingkaran dengan diameter 20 cm. (Jawaban: Jari-jari = 10 cm, Luas = πr 2 = π(10 2) = 314 cm 2)
Contoh Soal Cerita Lingkaran
Memahami konsep lingkaran tak melulu soal rumus dan angka. Contoh soal cerita justru membantu kita menghubungkan konsep abstrak ke dalam situasi nyata. Mari kita telusuri bagaimana soal cerita lingkaran dapat dipahami dan dipecahkan dengan lebih mudah.
Contoh Soal Cerita 1
Sebuah taman berbentuk lingkaran dengan diameter 14 meter. Di sekeliling taman tersebut akan dipasang pagar. Berapa panjang pagar yang dibutuhkan?
Ilustrasi: Bayangkan taman berbentuk lingkaran dengan garis tengah (diameter) 14 meter. Pagar akan mengelilingi taman tersebut. Kita perlu mencari keliling lingkaran untuk mengetahui panjang pagar yang dibutuhkan.
- Identifikasi informasi: Diameter lingkaran adalah 14 meter. Kita perlu mencari keliling.
- Mencari jari-jari: Jari-jari (r) adalah setengah dari diameter, sehingga r = 14 meter / 2 = 7 meter.
- Menggunakan rumus keliling lingkaran: Keliling = 2 × π × r. Dengan menggunakan pendekatan π = 22/7, maka Keliling = 2 × (22/7) × 7 = 44 meter.
- Kesimpulan: Panjang pagar yang dibutuhkan adalah 44 meter.
Contoh Soal Cerita 2
Sebuah roda sepeda memiliki jari-jari 25 cm. Jika roda tersebut berputar 10 kali, berapa jarak yang ditempuh sepeda?
Ilustrasi: Bayangkan sebuah roda sepeda yang berputar. Setiap putaran roda sepeda akan menempuh jarak sama dengan keliling roda. Kita perlu mencari keliling roda dan mengalikannya dengan jumlah putaran.
- Identifikasi informasi: Jari-jari roda adalah 25 cm dan jumlah putaran adalah 10 kali. Kita perlu mencari keliling roda dan jarak yang ditempuh.
- Mencari keliling roda: Keliling = 2 × π × r. Dengan menggunakan pendekatan π = 3,14, maka Keliling = 2 × 3,14 × 25 cm = 157 cm.
- Mencari jarak yang ditempuh: Jarak = Keliling × Jumlah putaran = 157 cm × 10 = 1570 cm.
- Kesimpulan: Jarak yang ditempuh sepeda adalah 1570 cm atau 15,7 meter.
Contoh Soal Cerita 3
Sebuah lapangan berbentuk lingkaran dengan luas 616 m². Berapa meter panjang diameter lapangan tersebut?
Ilustrasi: Bayangkan sebuah lapangan berbentuk lingkaran dengan luas 616 m². Kita perlu mencari jari-jari untuk menentukan diameter lapangan.
- Identifikasi informasi: Luas lingkaran adalah 616 m². Kita perlu mencari diameter.
- Menggunakan rumus luas lingkaran: Luas = π × r². Dengan menggunakan pendekatan π = 22/7, maka 616 = (22/7) × r². Mencari r²: r² = (616 × 7) / 22 =
196. Mencari r
r = √196 = 14 meter.
- Mencari diameter: Diameter = 2 × r = 2 × 14 = 28 meter.
- Kesimpulan: Panjang diameter lapangan adalah 28 meter.
Perbandingan Soal Cerita dan Soal Numerik
| Aspek | Soal Cerita | Soal Numerik |
|---|---|---|
| Konteks | Berkaitan dengan situasi nyata. | Tidak berkaitan dengan situasi nyata. |
| Informasi | Memerlukan identifikasi informasi yang relevan. | Informasi langsung diberikan. |
| Proses | Memerlukan pemahaman konsep dan penerapan rumus. | Penerapan rumus langsung. |
| Tujuan | Menerapkan pemahaman konsep ke situasi nyata. | Melatih kemampuan menghitung. |
Ilustrasi Visual
Memahami konsep lingkaran tidak hanya tentang rumus dan definisi. Penggunaan ilustrasi visual sangat penting untuk memperjelas pemahaman dan mengaitkannya dengan kehidupan sehari-hari. Visualisasi membantu dalam menyerap informasi dengan lebih efektif dan menjadikan pembelajaran lebih menarik.
Berbagai Ukuran dan Posisi Lingkaran
Memvisualisasikan lingkaran dengan beragam ukuran dan posisi akan membantu anak memahami bahwa lingkaran tidak hanya satu bentuk, tetapi dapat bervariasi. Bayangkan sebuah lingkaran kecil yang melambangkan bola pingpong, lingkaran sedang yang melambangkan roda sepeda, dan lingkaran besar yang melambangkan planet Bumi. Posisi lingkaran juga beragam, bisa di atas, di bawah, atau di tengah. Memvisualisasikan berbagai posisi akan melatih anak dalam membayangkan lingkaran dalam konteks ruang.
Penerapan Lingkaran dalam Kehidupan Sehari-hari
Lingkaran hadir di berbagai aspek kehidupan. Kita bisa menemukannya pada roda sepeda, jam dinding, koin, dan bahkan pada irisan buah. Bayangkan ilustrasi roda sepeda yang berputar, jam dinding yang menunjukkan waktu, atau koin yang berputar dalam permainan. Ilustrasi visual seperti ini membantu anak menghubungkan konsep abstrak lingkaran dengan objek-objek yang familiar dan nyata dalam kehidupan sehari-hari.
Perbandingan dengan Bentuk Geometri Lain
Memvisualisasikan perbandingan lingkaran dengan bentuk geometri lain akan membantu anak mengenali karakteristik unik lingkaran. Ilustrasi dapat berupa gambar persegi, segitiga, dan lingkaran yang disusun berdampingan, menunjukkan perbedaan bentuk dan ukurannya. Perbandingan ini dapat membantu anak memahami bahwa lingkaran memiliki karakteristik yang membedakannya dari bentuk geometri lainnya, seperti garis lengkung yang kontinyu.
Menyelesaikan soal lingkaran di kelas 6 memang menantang, ya? Kita perlu memahami rumus dan konsepnya dengan baik. Nah, untuk mengasah pemahaman dasar bahasa Indonesia, mengapa tidak mencoba soal kelas 1 SD bahasa Indonesia ? Latihan soal-soal sederhana itu bisa membantu melatih kemampuan berpikir logis yang penting juga dalam menyelesaikan soal lingkaran kelas 6. Dengan dasar yang kuat, kita pasti bisa menguasai konsep lingkaran dengan lebih baik lagi.
Menghitung Keliling dan Luas Lingkaran
Ilustrasi visual sangat membantu dalam memahami konsep keliling dan luas lingkaran. Bayangkan sebuah lingkaran dengan jari-jari tertentu. Ilustrasi dapat berupa lingkaran yang dibagi menjadi beberapa bagian kecil yang membentuk persegi panjang untuk menghitung luas. Gambar garis keliling lingkaran akan menunjukkan bagaimana menghitung keliling dengan rumus yang tepat.
Mengidentifikasi Unsur-unsur Lingkaran
Untuk mengidentifikasi unsur-unsur lingkaran, ilustrasi visual dapat berupa lingkaran dengan jari-jari, diameter, titik pusat, dan busur yang ditandai dengan jelas. Ilustrasi ini akan membantu anak memahami dan mengingat setiap bagian dari lingkaran, dan akan menghubungkan konsep dengan representasi visual yang tepat.
Latihan Soal Lingkaran
Menguasai konsep lingkaran tak hanya tentang menghafal rumus, tetapi juga memahami penerapannya dalam kehidupan sehari-hari. Latihan soal berikut dirancang untuk mengasah pemahaman Anda tentang lingkaran, mulai dari perhitungan sederhana hingga penerapan dalam soal cerita.
Soal Latihan Perhitungan Keliling dan Luas
Berikut beberapa soal untuk melatih pemahaman Anda dalam menghitung keliling dan luas lingkaran. Penting untuk memperhatikan satuan yang digunakan dalam perhitungan.
| No | Soal | Petunjuk |
|---|---|---|
| 1 | Jika jari-jari sebuah lingkaran adalah 7 cm, berapakah keliling dan luas lingkaran tersebut? | Gunakan rumus keliling = 2πr dan luas = πr2. Perhatikan satuan hasilnya. |
| 2 | Sebuah taman berbentuk lingkaran dengan diameter 20 meter. Berapa keliling taman tersebut? | Ingat, diameter = 2 x jari-jari. |
| 3 | Jika luas lingkaran adalah 154 cm2, berapakah jari-jarinya? | Gunakan rumus luas = πr2 dan selesaikan persamaan untuk mencari r. |
Soal Cerita Berkaitan Lingkaran
Berikut beberapa soal cerita yang mengaitkan konsep lingkaran dengan situasi nyata.
- Seorang tukang roti ingin membuat roti berbentuk lingkaran dengan diameter 14 cm. Jika ia ingin membuat 5 roti, berapakah luas keseluruhan roti yang dibutuhkan?
- Sebuah roda sepeda memiliki jari-jari 35 cm. Jika roda tersebut berputar sebanyak 10 kali, berapa jarak yang ditempuh sepeda?
- Sebuah taman berbentuk lingkaran memiliki keliling 88 meter. Berapa luas taman tersebut?
Soal Unsur-Unsur Lingkaran
Latihan ini berfokus pada pemahaman Anda tentang unsur-unsur lingkaran, seperti jari-jari, diameter, dan titik pusat.
- Gambarlah sebuah lingkaran. Tandai dan beri nama titik pusat, jari-jari, dan diameternya.
- Jika diameter lingkaran adalah 26 cm, berapa panjang jari-jarinya?
- Jelaskan perbedaan antara jari-jari dan diameter suatu lingkaran.
Tips Belajar Lingkaran
Menguasai konsep lingkaran bukan sekadar menghafal rumus, melainkan memahami maknanya. Dengan pemahaman yang mendalam, mengerjakan soal-soal lingkaran akan terasa lebih mudah dan menyenangkan. Berikut ini beberapa tips efektif untuk memahami dan menguasai konsep lingkaran.
Memahami Konsep Dasar Lingkaran
Membangun fondasi yang kuat sangat penting. Jangan terburu-buru ke rumus-rumus kompleks. Mulailah dengan memahami elemen-elemen dasar lingkaran seperti jari-jari, diameter, dan keliling. Visualisasikan lingkaran dalam berbagai bentuk dan situasi. Bayangkan bagaimana jari-jari, diameter, dan keliling saling berkaitan.
Menarik, bukan, soal lingkaran di kelas 6? Kita seringkali terpaku pada rumus-rumus dan contoh soal, tapi tahukah Anda bahwa konsep-konsep geometris, seperti lingkaran, bisa dihubungkan dengan hal-hal yang lebih luas? Misalnya, wukuf di Padang Arafah merupakan salah satu dari rangkaian ibadah haji yang mendalam dan penuh makna. wukuf di padang arafah merupakan salah satu dari prosesi spiritual yang mengharuskan pemahaman mendalam tentang makna dan tujuan hidup.
Pada akhirnya, mempelajari lingkaran di kelas 6 juga mengajarkan kita untuk memahami keterkaitan berbagai aspek kehidupan, seperti bagaimana setiap elemen saling terhubung dan membentuk suatu kesatuan yang utuh.
- Pelajari definisi setiap elemen dengan cermat.
- Buatlah sketsa lingkaran dan beri label pada elemen-elemennya.
- Hubungkan elemen-elemen tersebut dengan contoh nyata, seperti roda sepeda atau piring.
Menggunakan Visualisasi dan Analogi
Menggunakan gambar dan analogi dapat memperjelas konsep lingkaran. Misalnya, bayangkan lingkaran sebagai roda yang berputar. Diameternya seperti garis tengah roda, jari-jarinya seperti jarak dari pusat ke tepi roda, dan kelilingnya seperti panjang lintasan yang dilalui roda saat berputar.
- Gambarlah berbagai bentuk lingkaran dan beri keterangan pada setiap bagiannya.
- Hubungkan konsep lingkaran dengan benda-benda di sekitar kita, seperti roda mobil, bola, atau jam dinding.
- Buatlah diagram atau model tiga dimensi untuk memperjelas konsep.
Menguasai Rumus Lingkaran Secara Terstruktur
Rumus lingkaran dapat diingat dengan lebih mudah jika dipelajari secara bertahap dan terstruktur. Mulailah dengan rumus yang paling dasar, kemudian tingkatkan ke rumus yang lebih kompleks. Jangan mencoba menghafal semua rumus sekaligus. Pahami bagaimana rumus-rumus tersebut diturunkan dan kaitannya dengan elemen-elemen lingkaran.
- Hafal rumus keliling lingkaran (K = πd atau K = 2πr).
- Pahami bagaimana rumus luas lingkaran (L = πr2) diturunkan dari rumus keliling.
- Latih berulang kali dengan mengerjakan berbagai contoh soal.
- Buatlah catatan ringkas tentang rumus-rumus yang telah dipelajari.
Menerapkan Tips dalam Praktik
Setelah mempelajari konsep dasar, visualisasi, dan rumus, praktikkan dengan mengerjakan soal-soal latihan. Mulailah dengan soal-soal yang sederhana, kemudian tingkatkan kesulitannya secara bertahap. Jangan takut untuk bertanya kepada guru atau teman jika mengalami kesulitan. Jangan ragu untuk mencoba strategi yang berbeda sampai menemukan cara yang paling efektif untuk Anda.
| Tips | Contoh Penerapan |
|---|---|
| Memahami definisi setiap elemen lingkaran | Mendefinisikan jari-jari, diameter, dan keliling lingkaran dalam kata-kata sendiri. |
| Menggunakan visualisasi dan analogi | Membayangkan lingkaran sebagai roda sepeda dan menghubungkan elemen-elemennya dengan bagian-bagian roda. |
| Menguasai rumus lingkaran secara terstruktur | Menurunkan rumus luas lingkaran dari rumus keliling lingkaran. |
| Menerapkan tips dalam praktik | Mengerjakan soal-soal latihan lingkaran secara bertahap, dari soal yang mudah hingga soal yang sulit. |
Perbedaan dan Kaitan dengan Bentuk Geometri Lain
Lingkaran, meskipun tampak sederhana, memiliki hubungan yang menarik dan kompleks dengan bentuk geometri lainnya. Kita akan menjelajahi bagaimana lingkaran berbeda dengan bentuk seperti persegi dan segitiga, serta bagaimana ia terintegrasi dan diterapkan dalam berbagai bentuk geometri lainnya.
Perbandingan Lingkaran dengan Bentuk Geometri Lain
Berikut ini adalah perbandingan singkat antara lingkaran dengan beberapa bentuk geometri lainnya:
| Atribut | Lingkaran | Persegi | Segitiga |
|---|---|---|---|
| Bentuk | Melengkung, simetris terhadap semua diameter | Empat sisi yang sama panjang dan empat sudut siku-siku | Tiga sisi dan tiga sudut |
| Sisi | Tidak memiliki sisi yang lurus | Empat sisi lurus | Tiga sisi lurus |
| Sudut | Tidak memiliki sudut | Empat sudut siku-siku | Tiga sudut yang jumlahnya 180 derajat |
| Luas | πr2 | s2 | ½ × alas × tinggi |
Perbedaan mendasar terletak pada bentuk, keberadaan sisi dan sudut, serta rumus yang digunakan untuk menghitung luasnya. Lingkaran memiliki bentuk melengkung yang kontras dengan bentuk sudut yang dimiliki persegi dan segitiga.
Kaitan Lingkaran dengan Bentuk Geometri Lain
Lingkaran dan bentuk geometri lainnya saling berkaitan. Kita dapat menemukan lingkaran sebagai elemen dalam berbagai bentuk geometri.
Soal lingkaran kelas 6, seringkali melibatkan pemahaman konsep dasar geometri. Namun, bagaimana jika kita kaitkan dengan dunia nyata? Misalnya, otoritas jasa keuangan OJK adalah lembaga yang independen artinya, berfungsi untuk mengawasi dan mengatur industri jasa keuangan agar berjalan lancar. Kemandirian ini ibarat jari-jari lingkaran yang tak terpengaruh faktor eksternal, sehingga lingkaran tersebut dapat mempertahankan bentuk dan ukurannya.
Oleh karena itu, pemahaman tentang lingkaran tak hanya tentang rumus dan gambar, namun juga tentang prinsip-prinsip yang berlaku dalam kehidupan, seperti independensi. otoritas jasa keuangan ojk adalah lembaga yang independen artinya Hal ini pada akhirnya dapat membantu kita memahami soal lingkaran kelas 6 dengan lebih menyeluruh.
- Lingkaran dalam Persegi: Lingkaran dapat dibentuk di dalam persegi dengan jari-jari yang setengah dari sisi persegi. Ini menggambarkan keterkaitan dimensi antara keduanya.
- Lingkaran dalam Segitiga: Lingkaran dapat juga dibentuk di dalam segitiga. Lingkaran tersebut disebut lingkaran dalam segitiga.
- Lingkaran dan Jari-jari dalam Bangun Datar Lain: Konsep jari-jari dapat ditemukan dalam bentuk-bentuk lain, meskipun mungkin tidak selalu terlihat sebagai lingkaran utuh. Misalnya, dalam sebuah tabung, lingkaran berperan sebagai penampang melintang.
- Lingkaran dan Ukuran Bangun Datar Lain: Ukuran lingkaran (diameter, jari-jari) dapat digunakan untuk menentukan ukuran bentuk geometri lainnya. Misalnya, kita dapat menentukan diameter lingkaran yang sesuai dengan keliling persegi.
Lingkaran dapat menjadi bagian integral dari bentuk-bentuk geometri yang lebih kompleks. Perhatikan bagaimana lingkaran dapat menjadi elemen pembentuk dalam bangun datar yang lebih rumit.
Penerapan Lingkaran dalam Bentuk Geometri Lain
Lingkaran memiliki banyak penerapan dalam bentuk geometri lain, dari desain arsitektur hingga perhitungan fisika. Sebagai contoh, dalam arsitektur, lingkaran dapat dipadukan dengan bentuk-bentuk lain untuk menciptakan bangunan yang simetris dan indah.
- Roda: Bentuk lingkaran yang memutar menjadi sangat penting dalam roda, yang memungkinkan pergerakan benda.
- Jam: Lingkaran digunakan untuk menunjukkan waktu, dengan angka-angka yang menunjukkan posisi di sepanjang keliling.
- Benda-benda yang Berputar: Pergerakan melingkar atau berputar dalam bentuk-bentuk geometri lain. Perhatikan bagaimana lingkaran membentuk bagian inti dari roda gigi.
Contoh-contoh ini memperlihatkan bagaimana lingkaran berperan penting dalam berbagai aspek kehidupan.
Ilustrasi Visual (Gambaran)
Bayangkan sebuah persegi. Jika kita menggambar lingkaran di dalam persegi, dengan jari-jari yang setengah dari sisi persegi, maka kita melihat keterkaitan dimensi antara lingkaran dan persegi. Bayangkan juga sebuah segitiga. Lingkaran dapat dibentuk di dalam segitiga, menyinggung ketiga sisi segitiga. Ilustrasi ini menunjukkan bagaimana lingkaran dapat diintegrasikan dengan bentuk geometri lain.
Ringkasan Penutup
Melalui pembahasan soal lingkaran kelas 6 ini, diharapkan kamu dapat memahami konsep-konsep penting dan menerapkannya dalam menyelesaikan berbagai jenis soal. Dengan menguasai materi ini, kamu akan lebih siap menghadapi ujian dan mampu memecahkan masalah yang berkaitan dengan lingkaran dalam kehidupan sehari-hari. Selamat belajar!
Panduan FAQ: Soal Lingkaran Kelas 6
Bagaimana cara menghitung keliling lingkaran jika diketahui jari-jarinya?
Keliling lingkaran dihitung dengan rumus K = 2πr, di mana r adalah jari-jari.
Apa perbedaan antara keliling dan luas lingkaran?
Keliling lingkaran adalah panjang garis pembatas lingkaran, sedangkan luas lingkaran adalah daerah yang dibatasi oleh lingkaran tersebut.
Bagaimana cara mengidentifikasi informasi penting dalam soal cerita lingkaran?
Bacalah soal dengan cermat dan identifikasi variabel yang diketahui, seperti jari-jari, diameter, atau keliling. Perhatikan apa yang ditanyakan dalam soal.
Apakah ada contoh soal cerita yang melibatkan penerapan rumus keliling dan luas lingkaran?
Tentu, akan ada contoh soal cerita dalam materi ini.